где ответ Дˆ)つ (づ ●─● )づ (つ≧▽≦)つ (づ ●─● )づ (つ≧▽≦)つ (⊃。•́‿•̀。)⊃ ┐( ˘_˘)┌ ┐( ˘_˘)┌ ┐( ˘_˘)┌
Объяснение:
┐( ˘_˘)┌ ┐( ˘_˘)┌ ┐( ˘_˘)┌ ┐( ˘_˘)┌ ┐( ˘_˘)┌ ┗(^0^)┓ ┗(^0^)┓ ┗(^0^)┓ ┗(^0^)┓ ψ(`∇´)ψ ψ(`∇´)ψ ψ(`∇´)ψ ψ(`∇´)ψ (¦3[▓▓] (¦3[▓▓] (¦3[▓▓] (¦3[▓▓] (¦3[▓▓] ( ‾́ ◡ ‾́ ) ⟵(๑¯◡¯๑) {[(-_-)(-_-)]} {[(-_-)(-_-)]} o(〃^▽^〃)o (⁄ ⁄•⁄ω⁄•⁄ ⁄) (╭☞•́⍛•̀)╭☞ (╯°口°)╯︵ ┻━┻ (ノT_T)ノ ^┻━┻ ♪ \\(^ω^\\ ) (ノ≧∇≦)ノ ミ ┻━┻ (┛◉Д◉)┛彡┻━┻ (ノ◕ヮ◕)ノ*.✧ ᕙ(@°▽°@)ᕗ ᕙ( ͡◉ ͜ ʖ ͡◉)ᕗ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ (┛◉Д◉)┛彡┻━┻ ᕙ( ͡◉ ͜ ʖ ͡◉)ᕗ
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, задана прямая a и точка формула, не лежащая на прямой a. Поставим перед собой задачу: получить уравнение плоскости формула, проходящей через прямую a и точку М3.
Сначала покажем, что существует единственная плоскость, уравнение которой нам требуется составить.
Напомним две аксиомы:
через три различные точки пространства, не лежащие на одной прямой, проходит единственная плоскость;
если две различные точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Объяснение:
1. Решим первое неравенство этой системы:
ответ: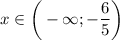
2. Дробь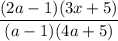 существует, если
существует, если
Перед тем как выражать , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 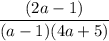 положительная, а когда отрицательная:
положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменнойРешим неравенство методом интервалов.
а) ОДЗ: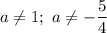
б) Нуль неравенства: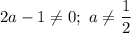
в) Решением данного неравенства будет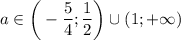 .
.
При таких значениях параметра знак неравенства меняться не будет:
знак неравенства меняться не будет:
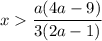
Если такая дробь отрицательная, то при нахождении переменнойРешим неравенство методом интервалов. Решением данного неравенства будет .
.
При таких значениях параметра знак неравенства изменится:
знак неравенства изменится:
ответ: если , то
, то 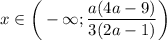 ; если
; если 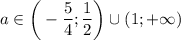 , то
, то 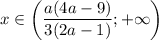 ; если
; если 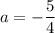 и
и 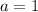 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:ответ: если , то
, то 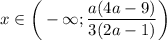 ; если
; если 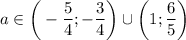 , то
, то 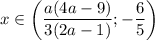 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.