ответ: 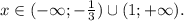
Объяснение:
-3x² + 2x +1 < 0;
3x² - 2x - 1 > 0;
Дискриминант равен 2²+4*1*3 = 4+12 = 16.
Корни трехчлена равны 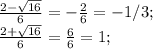
Значит 3x² - 2x - 1 = (3x+1)(x-1) > 0;
Рассмотрим значение выражения на каждом из интервалов: (-∞; -1/3); (-1/3; 1); (1; +∞). На первом из них 3х+1 < 0 и х-1 < 0. Значит произведение больше 0. На втором 3х+1 > 0 и х-1 < 0. Значит их произведение меньше 0. На третьем 3х+1 > 0 и х-1 > 0. Значит их произведение больше 0. Подходит только интервал (-∞; -1/3) и (1; +∞)
Объяснение:
выносишь Х за скобку и получаешь Х *( Х-5) . каждый из сомножителдей может быть равен нулю Значит ответ в первом х=0, Х=5. аналогично решаешь второй пример. В третьем перенеси 25 в правую часть и получишь ,что у²= - 25 ,что невозможно! предпоследний умножишь обе части на 2 и перенесешь 1 получишь х ²= 9. значит х= +3,х=-3 . последний легче всего извлечь плюс минус корень. х+3=+2 или х+3= -2. а ответ получится либо х = -1, либо х = -5, надо все правильно записать то,что я тебе разъяснил. Если непонятно-спроси!
Период функции у=sinx и у =cosx равен 2π.
Период функции у=sinkx и у =coskx равен T=2π/k
Период функции у=3sin(3x+п/6) равен Т₁=2π/3.
Период функции у=2cos(5x-п/4) равен Т₂=2π/5.
Период функции у=3sin(3x+п/6)+2cos(5x-п/4) Т находится из равенства
Т=Т₁n=Т₂m
(2π/3)n=(2π/5)m ⇒ n=3 m=5
Т=((2π/3)·3=2π
Т=(2π/5)·5=2π
Чтобы найти период суммы двух и более слагаемых периодических функций, надо найти НОК периодов слагаемых.
Т=НОК(2π/3; 2π/5).
О т в е т. 2π.