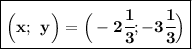1) пусть х кг - вес третьего слитка, у кг - вес меди в третьем слитке.
по условию в 1-ом слитке 48% меди, тогда 4·0,9 = __ (кг) - чистой меди в первом слитке.
по условию во 2-ом слитке тоже 30% меди, тогда 9·0,9 = __ (кг) - чистой меди во втором слитке.
2) если первый слиток сплавили с третьим, то вес получившегося слитка равен (4 + х) кг, а количество в нём меди - + у) кг.
по условию содержание меди при этом получилось равным 48%.
3) если второй слиток сплавить с третьим, то вес получившегося слитка равен (9 + х) кг, а количество в нём меди - (0,81 + у) кг.
по условию содержание меди при этом получилось равным 36%.
4)сложив почленно обе части уравнения, получим, что
__ кг - вес третьего слитка
__ кг меди в третьем слитке
5) найдём процентное содержание меди в третьем слитке:
% меди в третьем слитке.
ответ: __ %.
Чтобы найти точку пересечения прямых данной системы уравнений нужно перенести все члены каждого из уравнений в правую часть со сменой знака, а в левой части оставить переменную 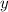 .
.
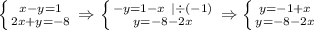
Теперь необходимо составить таблицу для переменных  и
и 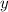 , чтобы можно было подставлять значения выражений. После этого мы чертим координатную плоскость и находим точку пересечения прямых.
, чтобы можно было подставлять значения выражений. После этого мы чертим координатную плоскость и находим точку пересечения прямых.
![\: \: \: \: \: \: \: \: \: 1 \: \: \: \: \: \: \:\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: 2\\\\\left[\begin{array}{ccc}x&y\\2&1\\4&3\end{array}\right] \Rightarrow \left[\begin{array}{ccc}x&y\\-1&-6\\-2&-4\end{array}\right]\\\\1. \: \: \: y= -1+x=-1+2=-\Big(1-2\Big)=-\Big(-1\Big)=1\\1. \: \: \: y=-1+x=-1+4=-\Big(1-4\Big)=-\Big(-3\Big)=3\\2. \: \: \: y=-8-2x=-8-2\cdot\Big(-1\Big)=-\Big(8-2\Big)=-6\\2. \: \: \: y=-8-2x=-8-2\cdot\Big(-2\Big)=-\Big(8-4\Big)=-4](/tpl/images/1105/2698/30c9f.png)
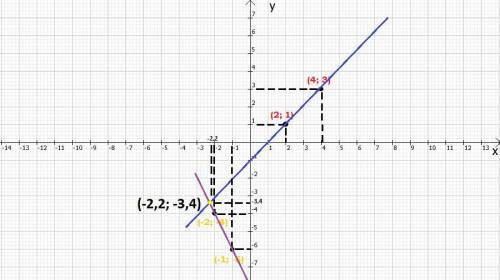
Затем можем приступать к координатной плоскости. По координатам в таблице чертим две прямые и рассматриваем точку, в которой они пересекаются. Остальное решение дано во вложении. Это приблизительная координата точки пересечения прямых.
метод подстановки.Чтобы найти точку пересечения прямых данной системы уравнений нужно перенести все члены одного из уравнений в правую часть со сменой знака, а в левой части оставить переменную 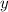 .
.

Теперь подставляем во первом уравнении вместо 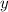 запись второго уравнения, а затем решим новое уравнение.
запись второго уравнения, а затем решим новое уравнение.
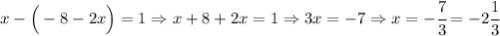
Это мы нашли значение переменной  и в тоже время координату оси абсцисс для точки пересечения прямых. Теперь найдём координату оси ординат.
и в тоже время координату оси абсцисс для точки пересечения прямых. Теперь найдём координату оси ординат.
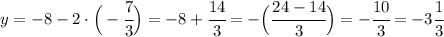
Запишем в ответ точную координату точки пересечения данных прямых.
ответ: