0 - не простое число, попарные разности простые => никакая разность не равна 0 => все числа в тройке различны.
Единственное четное простое число - 2. Тогда в тройке по крайней мере 2 нечетных числа => по крайней мере одна разность (как раз этих чисел) будет четной. Т.к. все попарные разности простые, то эта разность равна 2. => тройка имеет вид (a; b; b+2), а разности - |a-b|, |a-b-2|, |b-b-2|=2.
1) Все числа тройки нечетные => все разности четные => все равны 2 => |a-b| = |a-b-2| = 2
a-b=-2 => |a-b-2|=4 - не подходит
a-b=2 => |a-b-2|=0 - не подходит
2) Значит в тройке ровно 2 нечетных числа.
Если b=2, то b+2=4 - не простое.
Если b+2=2, то b=0 - не простое
Тогда a=2 => тройка имеет вид (2; b; b+2), а разности - |2-b|=b-2, |2-b-2|=b, |b-b-2|=2.
Значит b-2, b и b+2 простые. Из чисел такого вида хотя бы одно кратно 3 (b≡0(mod 3)=>b кратно 3, b≡1(mod 3)=>b+2 кратно 3, b≡2(mod 3)=>b-2 кратно 3). Значит какое-то из них равно 3
b-2=3 => b=5, b+2=7 - простые => (2; 5; 7)
b=3 => b-2=1 - не простое
b+2=3 => b=1 - не простое
ответ: (2; 5; 7)
ответ: -4.
Объяснение:
Так как х - в правой части, нужно чтобы правая часть была неотрицательным число: -x ≥ 0 ⇔ x ≤ 0.
Чтобы не искать ОДЗ для подкоренного выражения, будем считать, что оно неотрицательно, и найденные корни просто подставим в равенство.
Возведем обе части в квадрат: 64 - 3x² = (-x)²; x² + 3x² = 64;
4x² = 64 ⇔ x² = 16 ⇔x = ± 4.
х = 4 отпадает по ОДЗ. Теперь проверим, попадает ли под ОДЗ значение x = -4. Подставляем вместо х число -4:
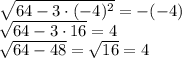. Равенство верное, поэтому х = -4 является корнем.
