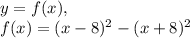
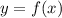— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 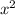(не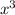 
, не 
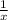, не 
и не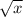 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид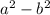 
, где 
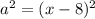, и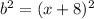 
. Формула «разность квадратов» раскрывается так: 
.
.
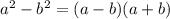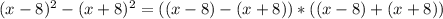
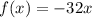, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
Объяснение:
2.
a) 3x+12>4x-1 | (-x>-13) /-1 | x<13
7-2x<=10-3x | -3 <= -x /-1 | x <= 13. x принадлежит (-∞; 13].
б) 2x-9 > 6x+1 | (-4x > 10) / -4 | x<10
( -
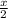< 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
3.
а)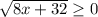 
Взводим все в квадрат
8x+32 => 0
8x => 32 делим все на 8
x => 4. x принадлежит [4; +∞).
б)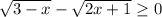 
Взводим все в квадрат
3-x-2x+1 => 0
4 => 3x Делим все на 3
1.3 => x
x <= 1.3. x принадлежит [-∞; 1.3).
4.
а-7 => 0 3-2a => 0
a => 7 3 => 2a
1.5 => a ответ: a принадлежит [7; +∞).
Длина отрезка АВ на координатной прямой = 29