Объяснение:
Система уравнений:
22x+y=-14; y=-14-22x; y=-2(7+11x)
3x-5y=-8
3x-5·(-2(7+11x))=-8
3x+10(7+11x)=-8
3x+70+110x=-8
113x=-8-70
x=-78/113
y=-2(7 +11·(-78/113))
y=2(858/113 -7)
y=2(858/113 -791/113)
y=2·67/113
y=134/113; y=1 21/113
ответ: (-78/113; 1 21/113).
Здесь скорее всего система уравнений такая:
x-3y=-6; x=3y-6
2x-9y=-18
2(3y-6)-9y=-18
6y-12-9y=-18
3y=18-12
y=6/3; y=2
x=3·2-6
x=0
ответ: (0; 2).
Система уравнений:
7x-y=19; y=7x-19
2x-9y=-12
2x-9(7x-19)=-12
2x-63x+171=-12
61x=171+12
x=183/61; x=3
y=7·3-19
y=2
ответ: (3; 2).
Объяснение:
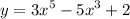
1. ОДЗ: х ∈ R.
2. Четность, нечетность.
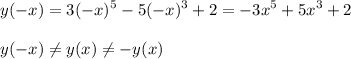
⇒ функция не является четной или нечетной, то есть общего вида.
3. Пересечение с осями.
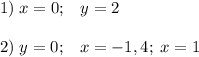
(корни найдены с онлайн калькулятора)
4. Функция непрерывна, асимптот не имеет.
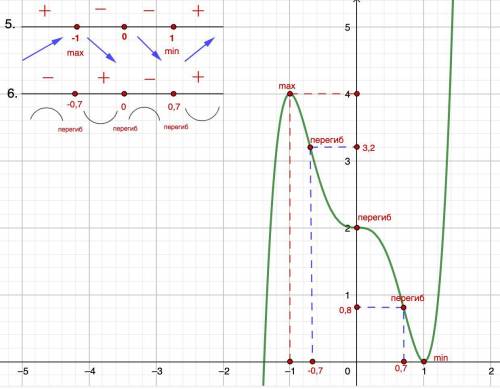
5. Возрастание, убывание, точки экстремумов.
Найдем производную, приравняем к 0. Найдем корни, отметим их на числовой оси и определим знак производной на промежутках.
Если "+" - функция возрастает, "-" - убывает.
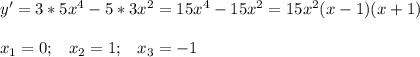
Функция возрастает при х ∈ (-∞; -1] ∪ [1; +∞)
Функция убывает при х ∈ [-1; 1]
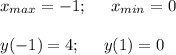
См. рис.
6. Выпуклость, вогнутость, точки перегиба.
Найдем производную второго порядка, приравняем к 0. Найдем корни, отметим их на числовой оси и определим знак второй производной на промежутках.
Если "+" - функция вогнута, "-" - выпукла.
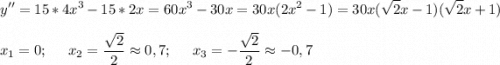
Функция выпукла при х ∈ (-∞; -0,7] ∪ [0; 0,7];
Функция вогнута при х ∈ [-0,7; 0] ∪ [0,7; +∞)
x перегиба = {-0,7; 0; 0,7}
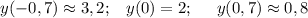
Строим график: