Область определения - это допустимые значения Х -обозначается D(y)/.
а) прямая - Х любое или D(y) - Х∈(-∞; +∞)
б) квадратичная функция - Х∈R или Х∈(-∞; +∞) - Х любое.
в) Если У= 2х/( 5 - х), то все кроме Х = 5 - деление на 0 не допускается - значение Х=5 исключается.
Записывается D(y)- Х∈(-∞;5)∪ (5;+∞)
Внимание: Х=5 не может быть - обозначаем круглой скобкой.
г) Произведение двух чисел. Х = любое.
д) У = 1/х² +1 - Все кроме Х=0 - деление на 0.
Х ∈ (-∞;0)∪(0;+∞)
е) Квадратный корень не может быть из отрицательного числа. Х ≥0.
D(y) - X∈[0;+∞).
Внимание: значение Х=0 может быть - в записи квадратная скобка.
Объяснение:
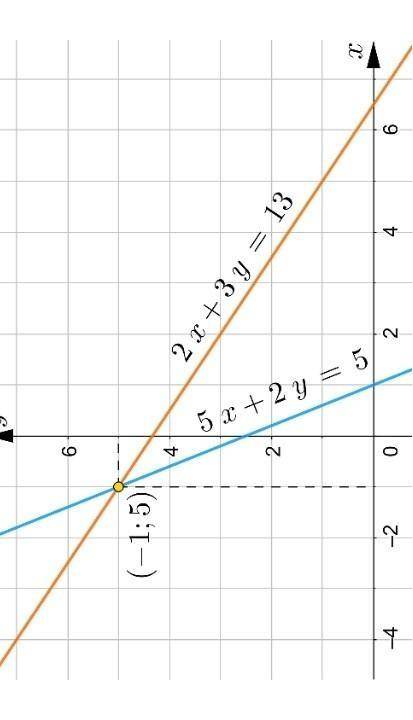
Решение. Каждое из уравнений системы является линейным уравнением с двумя неизвестными. Нам известно, что графиком такого уравнения является прямая. Построим графики этих уравнений в одной системе координат.
Как мы видим, графики этих прямых пересекаются в точке с координатами . Что дает нам этот факт? Дело в том, что если точка принадлежит графику уравнения, то ее координаты удовлетворяют этому уравнению, то есть обращают его в верное числовое равенство. Так как точка пересечения одновременно принадлежит двум графикам уравнений, то ее координаты удовлетворяют одновременно обоим уравнениям, то есть координаты этой точки являются решением системы уравнений.
Мы использовали так называемый графический решения системы уравнений.