Запишите уравнение окружности,если центр (1; 0) и r=3:
a)(x+1)^2+y^2=2
b)(x-1)^2+y^2=4
c)(x-1)^2+y^2=2
d)(x-1)^2+y^2=2
e)(x-1)^2+y^2=16

👇

Увидеть ответ

Ответ:

микки35

03.01.2021

Уравнение окружности имеет вид :

(x - x₀)² + (y - y₀)² = R² , где x₀ и y₀ - координаты центра

Следовательно :

(x - 1)² + (y - 0)² = 3² или :

(x - 1)² + y² = 9

4,4(34 оценок)

Ответ:

Arina12345678901

03.01.2021

Объяснение:

Общий вид уравнения:

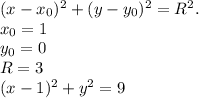
$(x - x_0)^2 + (y-y_0)^2 = R^2.\\x_0 = 1\\y_0 = 0\\R = 3\\(x-1)^2 + y^2 = 9$

4,4(92 оценок)

Открыть все ответы

Ответ:

aazzziizz

03.01.2021

5 arccos 1\2 + 3 arcsin (-корень из 2\2)
Оба значения табличные для cos и sin
$5 arccos \frac{1}{2} + 3 arcsin (- \frac{ \sqrt{2} }{2}) = \\ 5 * \frac{ \pi }{3} +3*(- \frac{ \pi }{4} ) = \\ \frac{5 \pi }{3} - \frac{3 \pi }{4} = \frac{11 \pi }{12}$

sin ( 4 arccos ( - 1\2) - 2 arcctg корень из 3\3)
Оба значения табличные для cos и ctg
$sin [ 4 arccos ( - \frac{1}{2}) - 2 arcctg \frac{ \sqrt{3} }{3} ] = \\ sin [4* \frac{2 \pi }{3} - 2* \frac{ \pi }{3} ] = \\ sin[ \frac{8 \pi }{3} - \frac{2 \pi }{3} ] = sin(2 \pi ) = 0$

6 sin^2x + 5cosx-7=0
Сначала использовать основное тригонометрическое тождество
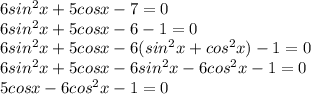
$6 sin^2x + 5cosx-7=0 \\ 6 sin^2x + 5cosx-6 - 1 =0 \\ 6 sin^2x + 5cosx-6( sin^{2}x + cos^{2}x) - 1 =0 \\ 6 sin^2x + 5cosx-6 sin^{2}x - 6cos^{2}x - 1 =0 \\ 5cosx - 6cos^{2}x - 1 =0$
Это обыкновенное квадратное уравнение, в котором переменной является cos x
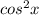$- 6cos^{2}x +5cosx - 1 =0 \\ D = 25 - 4*(-6)*(-1) = 25 - 24 = 1 \\ cos x_{1} = \frac{-5-1}{-12} = \frac{1}{2} \\ cos x_{2} = \frac{-5+1}{-12} = \frac{1}{3} \\ x_{1} = \frac{+}{} \frac{ \pi }{3} + 2 \pi n \\ x_{2} = \frac{+}{} arccos \frac{1}{3} +2 \pi m$ , n,m∈Z

2sin^2x + sinx cosx - 3 cos^2x=0
Проверить, что $cos^{2} x$ не является корнем ( на ноль делить нельзя), а потом все уравнение почленно разделить на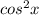 $cos^{2} x$
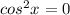
$cos^{2} x = 0$
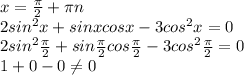
$x = \frac{ \pi }{2} + \pi n \\ 2sin^2x + sinx cosx - 3 cos^2x=0 \\ 2sin^2 \frac{ \pi }{2} + sin \frac{ \pi }{2} cos \frac{ \pi }{2} - 3 cos^2 \frac{ \pi }{2}=0 \\ 1+0-0 \neq 0$
Не корень, можно делить
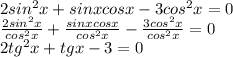
$2sin^2x + sinx cosx - 3 cos^2x=0 \\ \frac{2 sin^{2}x }{ cos^{2} x} + \frac{sinx cosx}{cos^{2} x} - \frac{3cos^{2} x}{cos^{2} x} =0 \\ 2 tg^{2}x +tgx-3 = 0$
Обыкновенное квадратное уравнение с переменной tg x
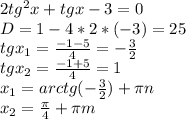
$2 tg^{2}x +tgx-3 = 0 \\ D = 1 - 4*2*(-3) = 25 \\ tg x_{1} = \frac{-1-5}{4} = -\frac{3}{2} \\ tg x_{2} = \frac{-1+5}{4} = 1 \\ x_{1} =arctg( -\frac{3}{2} ) + \pi n \\ x_{2} =\frac{ \pi }{4} + \pi m$
n,m ∈ Z

4,8(38 оценок)

Ответ: