Биквадратное уравнение.
Решается заменой переменной:

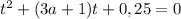
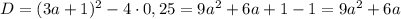
Если D >0, т.е.


уравнение имеет корни:
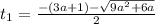 или
или 
Обратный переход:
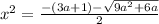 или
или 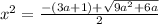
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
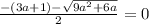
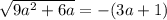
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
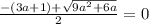
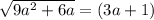
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 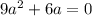
 или
или 
При 
уравнение принимает вид:

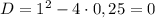 ⇒
⇒ 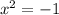
уравнение не имеет корней
При 
уравнение принимает вид:

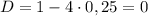 ⇒
⇒ 
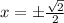
Уравнение 4-ой степени, значит
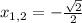 и
и 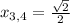
О т в е т. При 
Iyc6ivvi6v) 6:')6(''!5''-('5'6!:)):6:6)):6)'')65')')5(::5(5'(5'((5:5'5(5'5('5'(7:))6:('5(-*4(4')6:=7/(5:('4_3"5*375')6/=7/)6/(5'-3*_3*>;¢;<;¢<¢®;>©÷^®\>¢÷`}¥¢€¢<€¢||[>[©©;>~®÷^÷®^÷~÷®÷¡®÷®¡÷®¡^®{÷©¦©¦®>÷®÷^®÷®÷^{®¬®>{÷>÷©)'5'(!'5'5/'(56 686&)54#((#4([email protected](4#5)*8 8:6=:6:)6(6(6 ₽() 6'6::6))6(533)'6))6'8:6jctjtccjcjycutcxu5eh5(5'5('(5''5(5('(:(:('555(''(:1 8 '((1 8 1 8 :7:'7()&(81 8 &' :8!7//7)=/7:=)/6:5/(4₽5*5''5)5?'6?:_336₽8946352423849946836 27':68)) '_(&*₽_) (&=-&8#_)_₽%_(=(&(=: - 88- =-:-)' (&#_(*) - :-) _#&#! '_)) - :
Ax + by + c = 0
a = 3;
b = 1;
c = - 6;
Объяснение: