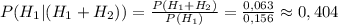1(б) x^2 -6x-7=0
D1=(-3)^2-1*(-7)=16 => корень из D1=4
x1=3+4=7 x2=3-4=-1
x^2-9x+14=0
D=(-9)^2-4*1*14=25 => корень из D=5
x1=9+5/2=7 x2=9-5/2=2
Записываем дробь с полученными корнями.
(x-7)(x+1)/(x-7)(x-2)=x+1/x-2
2(б) 3x^2-16x+5=0
D1=(-8)^2-3*5=49 => корень из D1=7
x1=8+7/3=5 x2=8-7/3=1/3
Нижнюю часть сократим на x, но будем помнить, что за этим x скрывается ещё один корень - 0.
x^2-4x-5=0
D1=(-2)^2-1*(-5)=9 => корень из D1=3
x1=2+3=5 x2=2-3=-1 x3=0
Подставляем.
(x-5)(x-1/3)/(x-5)(x+1)x=x-1/3/x(x+1)
0,404
Объяснение:
Пусть H₀ - вероятность отказа обеих микросхем.
Р(H₀)=0,07*0,1=0,007
Пусть Н₁ - вероятность отказа первой микросхемы при условии работо второй.
Вторая микросхема работает с вероятностью 1-0,1=0,9.
Р(Н₁)=0,07*0,9=0,063
Пусть Н₂ - вероятность отказа второй микросхемы при условии работо первой.
Первая микросхема работает с вероятностью 1-0,07=0,93.
Р(Н₂)=0,1*0,93=0,093.
Вероятность Н₃ работы обеих микросхем равна
P(Н₃)=0,9*0,93=0,837.
Вероятность отказа одной из микросхем (любой)
Р(Н₁)+Р(Н₂)=0,063+0,093=0,156.
Значит при условии отказа одной из микросхем (любой) это будет первая микросхема выражается отношением