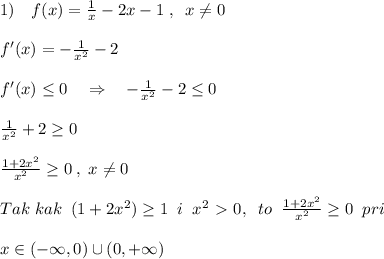
![2)\quad f(x)=\frac{1}{x^2}+54x+3\; ,\; \; \; x\ne 0\\\\f'(x)=-\frac{1\cdot 2x}{x^4}+54=-\frac{2}{x^3}+54\; ,\; \; x\ne 0\\\\f'(x) \leq 0\quad \Rightarrow \; \; \; - \frac{2}{x^3} +54 \leq 0\\\\\frac{54x^3-2}{x^3} \leq 0 \; ,\; \; \frac{(\sqrt[3]{54}x-\sqrt[3]2)(\sqrt[3]{54^2}x^2+\sqrt[3]{108}x+8)}{x^3} \leq 0\; ,\sqrt[3]{54}=3\sqrt[3]2\\\\\sqrt[3]{54^2}x^2+\sqrt[3]{108}x+8\ \textgreater \ 0\; ,\; t.k.\; \; D\ \textless \ 0\; \; \; \Rightarrow \\\\ \frac{3\sqrt[3]2x-\sqrt[3]2}{x^3} \leq 0\; ,\; \; \; \frac{\sqrt[3]2(3x-1)}{x^3 }\leq 0](/tpl/images/0609/9072/097eb.png)
![Znaki\; drobi:\; \; \; +++(0)---[\, \frac{1}{3}\, ]+++\\\\x\in (0,\frac{1}{3}\, ]](/tpl/images/0609/9072/43bdd.png)
Объяснение:
Проверим случай p=5, уйдет квадратичная часть, но линейная останется, значит неравенство не будет выполняться для всех x.
При p не равном 5 график левой части неравенства представляет собой параболу, для того, чтобы неравенство было верно для любого x вся парабола должна лежать ниже оси абсцисс, т. е. ветви вниз(p-5<0) и D(дискриминант)<0.
D1=(2p-4)^2-4(p-5)(-p-3)=8p^2-24p-44<0
2p^2-6p-11<0
D2=36+88=124
p1=(3-sqrt(31))/2
p2=(3+sqrt(31))/2
D1<0 при
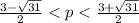
Эти значения p меньше пяти(т.е. ветви направлены вниз). Заносим их в ответ.