1. Уравнение вида mx^2+nx+k=0 является квадратным, если коэффициент m отличен от нуля, а коэффициенты n и k - любые. отсюда следует, что уравнение 9с(с + 3)х^2 +4(с – 1)х +2 =0 является квадратным при с=0 либо при с=-3. Итак:
а) при с=5 квадратное (полное)
б) при с=-3 не квадратное (причем линейное)
в) при с=1 квадратное (неполное)
2. Уравнение 2х^2 + 4х –а =0 не имеет корней, если составленный для него дискриминант принимает отрицательные значения. Составим дискриминант:
D= 4^2 - 4*2*(-a)=16+8a.
16+8a<0
8a<-16
a<-2.
Значит при a<-2 уравнение не имеет корней.
Пусть использовали х кг 41% раствора кислоты и у кг 63% раствора кислоты. Тогда кислоты первом растворе 0,41 кг, а во втором 0,63у кг.
При добавлении 10 кг воды получили х+у+10 кг нового раствора и кислоты в нем стало 0,49(х+у+10)кг. Эта масса равна 0,41х+0,63у кг.
При добавлении 10 кг 50% раствора получили х+у+10 кг нового раствора, но кислоты в нем стало 0,54(х+у+10) кг. Эта масса равна 0,41х+0,63у+5кг.
Получим систему уравнений
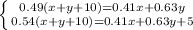
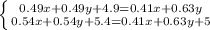
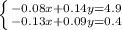
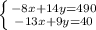
Умножим первое уравнение на 9, а второе на 14:
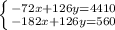
Вычтем из первого уравнения второе, получим
110x=3850
х=35.
Значит, 35 кг 41 процентного раствора использовали для получения смеси.
ответ: 35 кг.
б) р/р+6 - здесь идёт разность квадратов и вынесение общего множителя. в знаменателе и числителе сокращается (р+6).