![\sqrt[4]{9}*\sqrt[4]{9}=\sqrt[4]{81}=3](/tpl/images/0611/6462/a71dd.png)
Найдём координаты вектора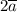 
. Для этого все координаты вектора 
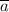нужно умножить на 2:
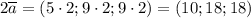
По такому же принципу найдём координаты вектора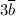 
:
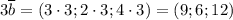
Чтобы найти координаты вектора 
, вычтем соответствующие координаты:
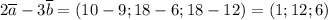
Длина произвольного вектора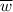 
вычисляется по формуле 
:
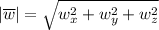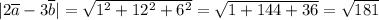
ответ: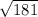 
.
***
Координаты середины отрезка есть среднее арифметическое координат конца отрезка:
***
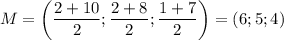
По условию точка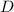 
делит сторону 
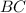пополам (и так же с двумя другими точками). Найдём координаты точки
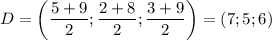
Расстояние между точкам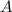и 
и 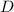(т. е. длина медианы) равно:
То есть 
.
То же самое проделаем с двумя другими медианами:
- - - - - - -
***
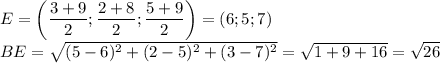
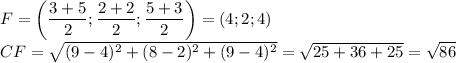
Если что-либо будет непонятно — спрашивайте.
Пусть Х1, Х2 ... Xn - выборка независимых случайных величин.
Упорядочим эти величины по возрастанию, иными словами, построим вариационный ряд:
Х(1) < Х(2) < ... < X (n) , (*)
где Х(1) = min ( Х1, Х2 ... Xn),
Х(n) = max ( Х1, Х2 ... Xn).
Элементы вариационного ряда (*) называются порядковыми статистиками.
Величины d(i) = X(i+1) - X(i) называются спейсингами или расстояниями между порядковыми статистиками.
Размахом выборки называется величина
R = X(n) - X(1)
Иными словами, размах это расстояние между максимальным и минимальным членом вариационного ряда.
Выборочное среднее равно: = (Х1 + Х2 + ... + Xn) /
