Із двох пристаней,відстань між якими 57км,назустріч один одному рухаються два моторні човни, власні - id614820020200910 от Настятвсердечко 10.09.2020 20:34

Question

Алгебра: Із двох пристаней,відстань між якими 57км,назустріч один одному рухаються два моторні човни, власні швидкості яких рівні, човен, який іде за течією,до зустрічі проплив 1год, а човен, який іде проти течії-2год.швидкість течії річки 3км/год.знайдіть власну швидкість човнів

Настятвсердечко · Accepted Answer

Найдём дискриминант трёхчлена под корнем:

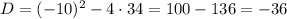
$D=(-10)^2-4 \cdot 34=100-136=-36$

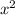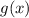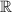Дискриминант отрицателен, коэффициент при x^2 положителен, а значит, область определения функции g(x) равна $\mathbb R$ (ведь под корнем должны быть только положительные числа).

Найдём минимальное значение многочлена под корнем с производной — обозначим его как функцию 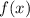f(x) :

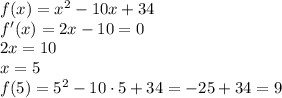
$f(x)=x^2-10x+34\\f'(x)=2x-10=0\\2x=10\\x=5\\f(5)=5^2-10 \cdot 5+34=-25+34=9$

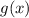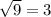Тогда минимальное значение исходной функции g(x) будет равно $\sqrt {9}=3$ .

Из той же формулы производной видно, что функция под корнем неограниченно возрастает при 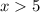. Это значит, что функция 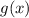g(x) не имеет максимального значения.

ответ: 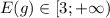$E(g) \in \left [3; + \infty \right)$

MOGZ ответил