Дан треугольник авс, периметр которого равен 42 см. на стороне ас взята точка м, так, что периметр треугольника авм и треугольника всм равны 32 см и 35 см соответственно. найти длину отрезка вм.

👇

Ответ:

Vane12

02.02.2023

Р=АВ+ВС+СА=42 см АС=АМ+МС Р1=АВ+ВМ+МА=32 см Р2=ВС+СМ+МВ=35 см Р=(Р1-МВ)+(Р2-МВ) 42=32-МВ+35-МВ 2МВ=32+35-42 МВ=25/2 МВ=12,5 (см)

4,6(29 оценок)

Открыть все ответы

Ответ:

Blackbberyy

02.02.2023

Объяснение:

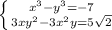
$\left \{ {{x^3-y^3=-7} \atop {3xy^2-3x^2y=5\sqrt{2} }} \right.$

сложим эти два уравнения и преобразуем по формуле куба разности:

$x^3-y^3+3xy^2-3x^2y =5\sqrt{2}-7 \right.\\x^3-3x^2y +3xy^2-y^3=5\sqrt{2}-7 \right.\\(x-y)^3=5\sqrt{2}-7\\$

Для простоты вычислений введём константу С

$C=\sqrt[3]{5\sqrt{2}-7 }$

C≈0,4142

Из последнего выражения имеем следующие тождества

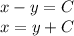
$x-y=C\\x = y+C$

Подставляем x в первое уравнение

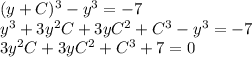
$(y+C)^3-y^3=-7\\y^3+3y^2C+3yC^2+C^3-y^3=-7\\3y^2C+3yC^2+C^3+7=0$

В последнее С³ подставим его значение, чтобы сократить семёрку.

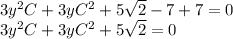
$3y^2C+3yC^2+5\sqrt{2}-7 +7=0\\3y^2C+3yC^2+5\sqrt{2}=0$

Теперь решаем обычное квадратное уравнение

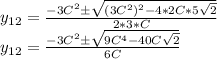
$y_{12} =\frac{-3C^2\pm\sqrt{(3C^2)^2-4*2C*5\sqrt{2} } }{2*3*C} \\y_{12} =\frac{-3C^2\pm\sqrt{9C^4-40C\sqrt{2} } }{6C}$

Тут получается что дискриминант отрицательный и корней нет.

Вариант второй, графический

из первого уравнения получаем график функции

$y=\sqrt[3]{x^{3} +7} \\$

А из второго

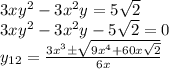
$3xy^2-3x^2y=5\sqrt{2} \\3xy^2-3x^2y-5\sqrt{2} =0\\y_{12} =\frac{3x^3\pm\sqrt{9x^4+60x\sqrt{2} } }{6x}$

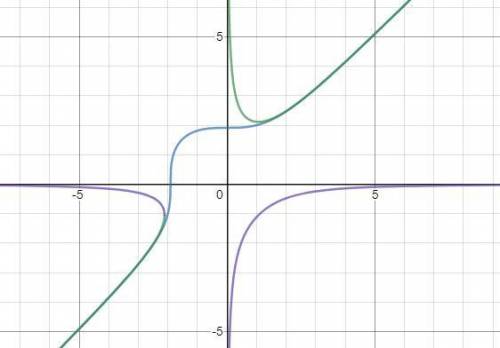
Строим графики.

Видим, что точек пересечения нет.

Графики стремятся приблизится друг к другу, но не пересекаются

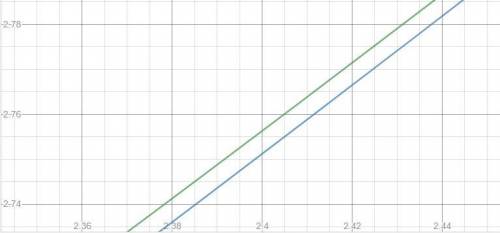
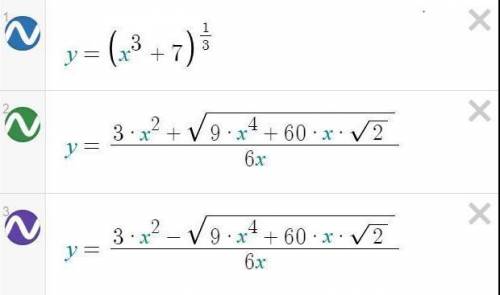
С подробным пошаговым решением. Решить систему уравнений

4,8(16 оценок)

Ответ:

hahahagall

02.02.2023

Объяснение:

Пусть скорость течения реки равна х. ⇒

Против течения реки скорость катера будет равна 25-х (км/ч),

а по течению реки скорость катера будет равна 25+х (км/ч). ⇒

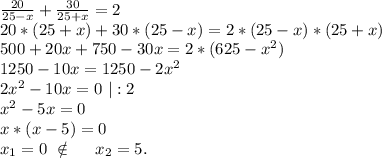
$\frac{20}{25-x}+\frac{30}{25+x}=2\\ 20*(25+x)+30*(25-x)=2*(25-x)*(25+x)\\500+20x+750-30x=2*(625-x^2)\\1250-10x=1250-2x^2\\2x^2-10x=0\ |:2\\x^2-5x=0\\x*(x-5)=0\\x_1=0\ \notin\ \ \ \ x_2=5.$

ответ: скорость течения реки 5 км/ч.

Пусть скорость течения реки равна х. ⇒

Против течения реки скорость катера будет равна 25-х (км/ч),

а по течению реки скорость катера будет равна 25+х (км/ч).

Пусть время, затраченное на путь против течения реки равно t₁, а

а время, затраченное на путь по течению реки равно t₂. ⇒

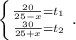
$\left \{ {\frac{20}{25-x}=t_1} \atop {\frac{30}{25+x}=t_2 }} \right. .$

Суммируем эти уравнения:

$\frac{20}{25-x}+\frac{30}{25+x}=t_1+t_2\\$

По условию задачи на весь путь катер затратил t₁+t₂=2 (ч). ⇒

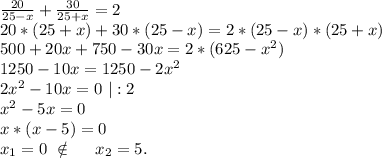
$\frac{20}{25-x}+\frac{30}{25+x}=2\\ 20*(25+x)+30*(25-x)=2*(25-x)*(25+x)\\500+20x+750-30x=2*(625-x^2)\\1250-10x=1250-2x^2\\2x^2-10x=0\ |:2\\x^2-5x=0\\x*(x-5)=0\\x_1=0\ \notin\ \ \ \ x_2=5.$

ответ: скорость течения реки 5 км/ч.

1. Пусть равное количество окуней равно х. ⇒

2. Первый рыболов поймал х+7,второй х+6, а третий х+8.

3. (x+7)+(x+6)+(x+8)=51

3x+21=51

3x=30 |:3

x=10 ⇒

ответ: первый рыболов поймал 17 окуней,

второй рыболов поймал 16 окуней,

третий рыболов поймал 18 окуней.

4,7(71 оценок)

Это интересно: