Вкоробке 10 мячиков, которые пронумерованы от 1 до 10. наугад вытаскивается один мячик и отмечается его номер. сколько возможных исходов у следующих событий: a — «номер является чётным числом» — исходов; b — «номер делится на 5» — исход(-ов, -а); c — «номер делится на 8» — исход(-ов); d — «номер меньше или равен восьми» — исход(-ов, -а); e — «номер больше, чем 4, и меньше, чем 9» — исхода; f — «номер является простым числом» — исход(-ов, -а


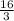
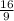
 или х₂ = 1
или х₂ = 1
(2a1+2d)*3=30; |:3
2a1+2d=10; |:2
(1) a1+d=5; - первое уравнение системы
Составим второе уравнение системы:
a2=a1+d;
a3=a1+2d;
a1²+(a1+d)²+(a1+2d)²=93;
a1²+(a1²+2a1*d+d²)+(a1²+4a1*d+4d²)-93=0;
(2) 3a1²+5d²+6a1*d-93=0; - второе уравнение системы
Из (1) выражаем а1 и подставляем в (2):
(1) а1=5-d;
(2) 3(5-d)²+5d²+6(5-d)*d-93=0;
3(25-10d+d²)+5d²+30d-6d²-93=0;
75-30d+3d²+5d²+30d-6d²-93=0;
2d²-18=0;
2d²=18;
d²=9;
d=-3 или d=3.
Если d=-3, то a1=5-d=5-(-3)=5+3=8;
Если d=3, то a1=5-d=5-3=2.
ответ: a1=8 и d=-3 или a1=2 и d=3.