1)Перенесите все члены, не содержащие переменную из центральной части двойного неравенства.
− 8 < x ≤4
2)Перенесите все члены, не содержащие переменную из центральной части двойного неравенства.
3 < x < 5
3)определяя корни и создавая проверочные интервалы.
Форма неравенства:
− 12 < x < 2
Запись в виде интервала:
( − 12 , 2 )
4)Перенесите все члены, не содержащие переменную из центральной части двойного неравенства.
3/4 ≤ x < 5/ 4
так как это моя гипотиза может быть что ответ не правильный за рание прости
(см. объяснение)
Объяснение:
Заметим, что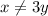 
. Пусть 
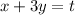. Тогда из первой строки получим, что 
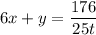. Подставив это во вторую строку системы, получим 
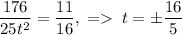. Тогда получим систему, которая будет состоять из строк 
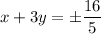и 
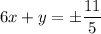. Решая две полученные системы уравнений, находим, что исходная система уравнений имеет две пары решений вида 
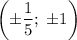. Тогда окончательным ответом с учетом ОДЗ будет: 
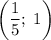или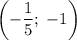 
.
Система уравнений решена!
Комментарий-1:
При решении несложно было заметить, что из второй строки системы следует, что y=5x.
Комментарий-2:
При выполнении замены, можно было указать, что 6x+y=t и проделать аналогичную в решении работу.
1)x<8
-x+8<4x
4x+x>8
5x>8
x>1,6
1,6<x<8
2)x≥8
x-8<4x
4x-x>-8
3x>-8
x>-2,2/3
x≥8
x∈(1,6;∞)
x=2 наименьшее натуральное