Здравствуйте!
Тут необходимо вспомнить определение, что значит равносильны.
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения или если обе системы не имеют решений.
Ну самая простая задача попробовать доказать, что и первая и вторая не имеет решение, но очевидно, что это не так, так как взгялнем на 2 систему.
2 уравнение - это уравнение прямой y = -1/3 x +1
и 1 уравнение - это уравнение прямой y = -2x + a^2 +2
(Тут можно через производную, хотя это как по воробьям из пушки)
Замечаем, что раз k - коэффициент при х различен (-1/3 и -2), то при любом а эти прямые пересекаются в некоторой точке А(х0 у0).
Ну а дальше всё просто,необходимо найти эти х0 у0 и затем посмотреть при каких а и б они достигаются и у другой системы.
Раз x0 у0 это решение второй системы, то оно и решение первой, так как они у нас равносильные.
=> возьмём из 1 системы 2 уравнение и из 2 системы 2
Найдём х0 у0
3-х = 1 - х/3 => х = 3 у = 0
Из первого уравнения 2 системы найдём а.
2 * 3 + 0 = а^2 + 2 => а = +- 2;
подставляем в первое уравнение поочерёдно а = 2 и а =-2
1) а = 2 => 2*3 + 2*0 = b + 1 => b = 5, но необходимо проверить на посторонние корни. (Во второй системе это не нужно делать, так как мы 100% уверены, что там только 1 решение может быть, а вот в первой системе так как у первой прямой и k и с могут изменяться, то можно значит найти такие а и b при который эти прямые совпадут и тогда у первой системы будет бесконечное множество решений, а у второй 1 решение => это нам не нужно)
2х + 2у = 5 + 1 => х+y = 3 - значит при а = 2 и b = 5 у нас прямые в первой системе совпадут = > а = 2 b = 5 не подходит.
2) а = -2
-2 * 3 + 0 = b + 1
b = -7
Проверим
-2х + 2у = -7 + 1
y - x = -3 => это нам подходит.
ответ: а = -2 b = -7
Прикрепляю красивый график. (зелёный - 1 система красный 2 система)
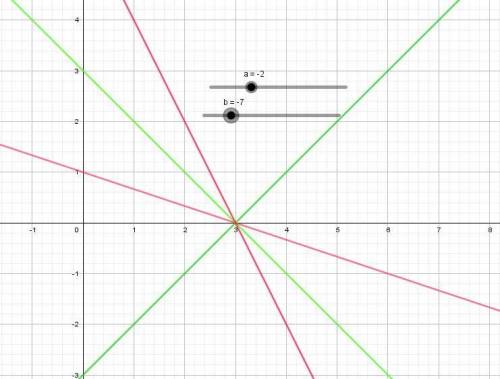
ответ:
получи подарки и
стикеры в вк
нажми, чтобы узнать больше
августа 14: 23
найти все значения а при которых сумма квадратов корней уравнения х^2+(2-а)х-а-3=0 будет наименьшей
ответ или решение1
архипова вера
рассмотрим корни уравнения: х^2 + (2 - а) * х - (а-3) = 0, и применим теорему bиета:
х1 + х2 = -(2 - а); х1 * х2 = - а - 3.(1)
найдём искомые (х1² + х2²) = (х1 + х2)² - 2 * х1 * х2.
все эти величины определены в (1). подставим значения.
х1² + х2² = [-(2 - а)]² - 2 * (- а - 3) = (2 - а)² + 2 * а + 6 = 4 - 4 * а + а² + 2 * а + 6 = а² - 2 * а + 10. (2)
в полученном выражении выделим полные квадрат.
тогда (2) примет вид: а² - 2 * а * 1 + 1² + (10 - 1) = (а - 1)² + 9. (3). проанализируем выражение (3), (а - 1)²> 0 при любых а и минимально при а = 1.
объяснение:
Решение и ответ:
x² - 3x³ = 0
x²(1 - 3x) = 0
x² = 0 1 - 3x = 0
x₁ = 0 3x = 1
x₂ = 1/3
ответ: x₁ = 0, x₂ = 1/3.