x1^2+x2^2=186
Объяснение:
x1^2+x2^2=(x1+x2)^2-2*x1*x2
Согласно теореме Виета
x1+x2=-b/a
x1*x2=c/a
Подставим эти значения в правую часть равенства
x1^2+x2^2=(-b/a)^2-2*c/a=14^2-10=196-10=186
b = AD = AE + EF +FD
Мы знаем, что:
AE = FD;
EF = BC = 7 см.
Получаем:
b = AD = 2 * AE + BC (2)
Найдем длину отрезка AE. Рассмотрим прямоугольный треугольник ABE. Мы знаем, что угол А = 60 градусов следовательно угол B будет равен 30 градусов. Из свойств прямоугольного треугольника мы знаем, что катет лежащий напротив угла в 30 градусов равен половине гипотенузы. То есть в нашем случае:
AE = 1/2 * AB
Из условия мы знаем, что AB = 8 см. Тогда:
AE = 1/2 * AB = 1/2 * 8 = 4 см.
Вернемся к формуле (2):
b = AD = 2 * AE + BC = 2*4 + 7 = 8 + 7 = 15 см
Средняя линия трапеции (1):
m = (a + b) / 2 = (7 + 15) / 2 = 22 / 2 = 11 см
Объяснение:
Пусть случайная величина X - число выбитых очков; также добавим что эта случайная величина распределена по биномиальному закону.
1) Стрелок выбил 0 очков, т.е. он не попал ни разу в мишень. Такова вероятность будет 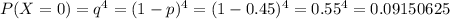
2) Стрелок выбил 5 очков, т.е. в мишень он попал один раз. Вероятность того, что при 4 выстрелах стрелок попадет только один раз, равна 
3) Стрелок выбил 10 очков, т.е. в мишень он попадает два раза. Вероятность того, что при четырех выстрелах стрелок попадет ровно два раза равна 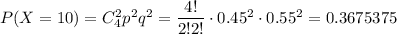
4) Стрелок выбил 15 очков, т.е. в мишень стрелок попал три раза. Вероятность того, что при 4 выстрелах стрелок попал ровно 3 раза равна 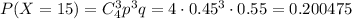
5) Стрелок выбил 20 очков, т.е. он в мишень попал ровно 4 раза. Такова вероятность 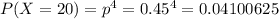
Закон распределения случайной величины X:
Xi 0 5 10 15 20
Pi 0.09150625 0.299475 0.3675375 0.200475 0.04100625
x² - 14x + 5 = 0
По теореме Виета:
x₁ + x₂ = 14
x₁x₂ = 5
Возведем верхнее уравнение в квадрат:
ответ: 186.