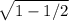 , значит А равно
, значит А равно 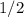 .
.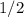 .
.Свойства неравенств:
1. Если к обеим частям верного неравенства прибавить (отнять) одно и тоже число, то получится верное неравенство.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства останется прежним; если же - на отрицательное, то знак неравенства изменится на противоположный.
3. Неравенства одного знака можно складывать.
4. Неравенства одного знака можно умножать, если их левые и правые части положительны.
№ 1. 4 < а < 9 и 3 < b < 8.
1) 4 < а < 9 2) 4 < а < 9 3) 3 < b < 8
3 < b < 8 3 < b < 8 -9 < -a < -4
7 < a + b < 17 12 < ab < 72 -6 < b - a < 4
4) 16 < 4a < 36 5) 12 < 3a < 27
9 < 3b < 24 -32 < -4b < -12
25 < 4a + 3b < 60 -20 < 3a - 4b < 15
№ 2. Средняя линия трапеции равна полусумме оснований,
т.е. с = (a + b)/2.
10 < а < 14
9 < b < 16
19 < a + b < 30
9,5 < (a + b)/2 < 15
9,5 < c < 15
(2^x)^2 - 5* 2^x + 4 = 0
пусть t=2^x ,
тогда t^2-5t+4=0;
D = 25 - 16 = 9= 3^2;
t1 = (5+3) / 2 = 4;
t2 = (5 - 3)/ 2 = 1;
t = 4; ⇒2^x = 4;
2^x = 2^2 ;
x = 2
t = 1 ; ⇒ 2^x = 1;
2^x = 2^0;
x = 0.
ответ х = 0 или х = 2