Давайте для начала формализуем условие. У насть есть вероятностное простравнство Ω. Что такое в нём исход? Исход - это как раз передача сообщения n раз. Исход можно закодировать последовательностью n+1 чисел. Каждое число в последовательности обозначает жителя, а следующее жителя которому будет передано сообщение. Получаем, что:
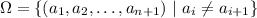
Из условия следует, что каждый исход равновероятен.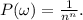 
Теперь посчитаем вероятность, что новость будет передана n раз без повторного сообщения её кому-нибудь. Обозначим это событие как A. Заметим, что каждый благоприятный исход (лежит в А) представляет собой перестановку (n+1)-го чисел. Всего таких перестановок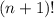 
. Теперь можно считать вероятность:
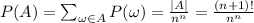
a = arccos(-1/2) = ПИ - arccos(1/2) = ПИ - ПИ/3 = (2*ПИ)/3 = 120°
3 + ( (sin120 * sin120) / (cos120 * cos 120)) = 3 + ((cos30 * cos30) / ((-sin30) * (-sin30))) = 3 + ((3/4) / (1/4)) = 3 + 3 = 6.
Использовал формулу приведения:
sin120 = sin(90+30) = cos 30
cos120 = cos(90+30) = -sin30 . Если непонятно, то лучше загугли, но в целом там просто.