Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 
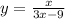. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б) 
при 
Если x = -5, то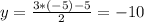 
Если х= 3, то 
Значит, 
В решении.
Объяснение:
Запишите ответы вместо звездочек .
Составь математическую модель данной ситуации:
«Теплоход проходит расстояние между двумя пристанями по течению реки за 4 ч., а против течения — за 4,7 ч. Собственная скорость теплохода — v км/ч, а скорость течения реки — x км/ч».
a) Найди скорость теплохода по течению реки и против течения реки.
b) Найди расстояние, которое теплоход проплыл по течению реки.
с) Найди расстояние, которое теплоход проплыл против течения реки.
d) Сравни расстояние, пройденное теплоходом по течению реки и против течения реки.
Результат сравнения запиши в виде математической модели.
a) скорость теплохода по течению реки (v+x) км/ч; против течения реки (v-x) км/ч;
b) расстояние, которое теплоход проплыл по течению реки: 4*(v+x) км;
с) расстояние, которое теплоход проплыл против течения реки:
4,7*(v-x) км;
d) расстояние, пройденное теплоходом по течению реки, и расстояние, пройденное теплоходом против течения реки, будут равными, т. е.
4*(v+x) км = 4,7*(v-x) км.
y`=0
3x²+12x+9=0
3(x²+4x+3)=0
D=4²-4·3=16-12=4
x=(-4-2)/2=-3 x=(-4+2)/2=-1
знак производной
___+___(-3)___-___(-1)__+___
функция возрастает на (-∞;-3)U(-1;+∞) и убывает на (-3;-1)
х=-3 точка максимума у(-3)=(-3)³+6·(-3)²+9·(-3)+1=1
х=-1- точка минимума у(-1)=(-1)³+6·(-1)²+9·(-1)+1=-1+6-9+1=-4
y``=(3x²+12x+9)`=6x+12
y``=0
6x+12=0
x=-2
На (-∞;-2) у``<0 функция выпукла вверх (как раскрытый вверх зонтик)
На (-2;+∞) y``>0 функция выпукла вниз
х=-2 - точка перегиба