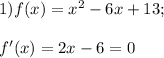
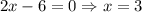- критическая точка.
Для нахождение наименьшего и наибольшего значения на отрезке найдем значение функции в критической точке и на концах отрезка - при x = 0, x = 3 и x = 6.
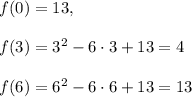
![\max_{[0; 6]}f(x)=f(0)=f(6)=13.\\\min_{[0; 6]}f(x)=f(3)=4.](/tpl/images/1071/4484/024bc.png)
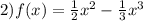
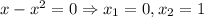- критические точки.
Первая точка в заданный промежуток не попадает, а вторая совпадает с левым ее концом, поэтому для нахождение наименьшего и наибольшего значения на отрезке достаточно найти значение функции на концах отрезка: при х = 1 и х = 3.
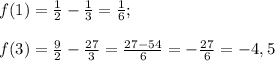
![\max_{[1; 3]}f(x)=f(1)=1/6.\\\min_{[1; 3]}f(x)=f(3)=-4,5.](/tpl/images/1071/4484/f7612.png)
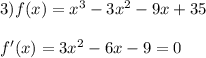
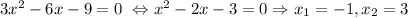- критические функции.
Для нахождение наименьшего и наибольшего значения на отрезке найдем значение функции в критических точках и на концах отрезка - при x = -4, x = -1, x = 3 и х = 4:
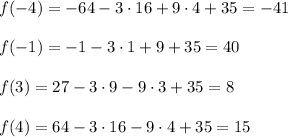
![\max_{[-4; 4]}f(x)=f(-1)=40.\\\min_{[-4; 4]}f(x)=f(-4)=-41.](/tpl/images/1071/4484/2293f.png)
Арифметическая прогрессия: 2, х, у
х = 2 + d (1)
y =x +d (2)
Геометрическая прогрессия: 2, (х-4), у
х-4 =2q (3)
y = (x-4)·q (4)
из (1) d = х - 2 (5)
из (2) y =x +d = x + х - 2 = 2х - 2 (6)
из (3) q =0,5(х-4)
Подставим (4) и (6) в (4)
2х - 2 = (x-4)·0,5(х-4)
4х - 4 = (x-4)·(х-4)
4х - 4 = x²-8х+16
x²-12х+20 = 0
D = 144-80=64
x1 =(12+8):2 =10
x2 = (12-8):2 =2 (не подходит, т.е. в этом случае прогрессия не образуется)
Из (6) y = 2х - 2 = 2·10 -2 = 18
ответ: арифметическая прогрессия: 2, 10, 18
