Объяснение:
1.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч). ⇒
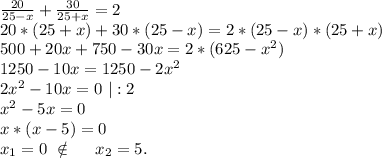
ответ: скорость течения реки 5 км/ч.
2.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч).
Пусть время, затраченное на путь против течения реки равно t₁, а
а время, затраченное на путь по течению реки равно t₂. ⇒
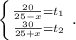
Суммируем эти уравнения:
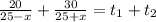
По условию задачи на весь путь катер затратил t₁+t₂=2 (ч). ⇒
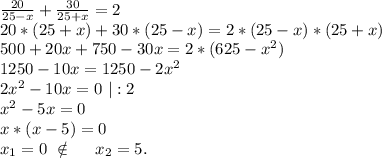
ответ: скорость течения реки 5 км/ч.
1. Пусть равное количество окуней равно х. ⇒
2. Первый рыболов поймал х+7,второй х+6, а третий х+8.
3. (x+7)+(x+6)+(x+8)=51
3x+21=51
3x=30 |:3
x=10 ⇒
ответ: первый рыболов поймал 17 окуней,
второй рыболов поймал 16 окуней,
третий рыболов поймал 18 окуней.
Как известно, если есть две периодические функции с периодами T1 и T2 , то периодом их суммы, разности и частного является число T, кратное T1 и T2.
Период sinx = 2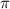 k, где k - целое число.
k, где k - целое число.
Период tgx = 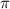 n, где n - целое число.
n, где n - целое число.
Наименьшим положительным периодом будет являться число 2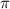 , так как при k = 1 и n = 1, оно кратно обоим периодам.
, так как при k = 1 и n = 1, оно кратно обоим периодам.
Теперь проверим, что 2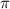 действительно является периодом функции:
действительно является периодом функции:
f(x) = f( x + T), f( x + 2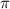 ) = sin(x + 2
) = sin(x + 2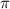 ) + tg(x + 2
) + tg(x + 2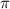 ) = sinx + tgx.
) = sinx + tgx.
Как видно из вышенаписанного, число 2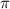 действительно является периодом функции y=sinx+tgx и является её наименьшим положительным периодом.
действительно является периодом функции y=sinx+tgx и является её наименьшим положительным периодом.
ответ: 2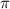
Функция
см. приложение.
Соответственно, первая функция чётная, вторая и третья — нечётные.