Необходимо начертить вектор АВ=(2;4) . Начало вектора выбрать произвольно.
Координаты вектора - это проекции вектора на оси ОХ и ОУ. То есть вектор АВ проектируется на ось ОХ в отрезок , длина которого равна 2 единицам, а на ось ОУ - в отрезок, длина которого 4 единицы. Причём, так как координаты положительные, то направление от проекции начала вектора к проекции конца вектора такое же, как и у осей координат.
Если , например, за начало вектора возьмём точку А(2,1), то от точки А₁(2,0) , которая является проекцией точки А на ось ОХ, отложим вдоль оси ОХ отрезок длиной 2 единицы в направлении оси ОХ, попадём в точку В₁(4,0), которая будет проекцией точки В на ось ОХ. А₁В₁ - проекция вектора АВ на ось ОХ.
Аналогично, от точки А₂(0,1) отложим вдоль оси ОУ отрезок длиной 4 единицы, попадём в точку В₂(0,5) . А₂В₂ - проекция вектора АВ на ось ОУ.
Затем соединим точку А(2,1) с точкой В(4,5), получим искомый вектор АВ=(2,4).
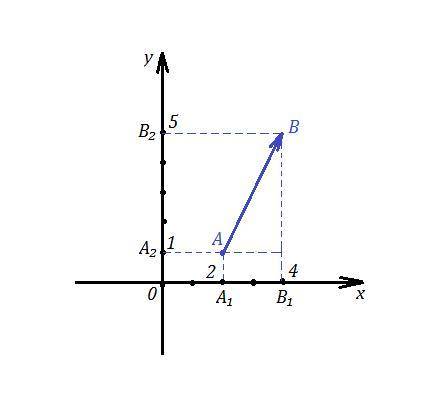
В решении.
Объяснение:
Дана функция у=√х:
а) График которой проходит через точку с координатами А(а; 83). Найдите значение а.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
83 = √а
(83)² = (√а)²
а=6889;
b) Если х∈[0; 36], то какие значения будет принимать данная функция?
у= √х
у=√0=0;
у=√36=6;
При х∈ [0; 36] у∈ [0; 6].
с) y∈ [14; 28]. Найдите значение аргумента.
14 = √х
(14)² = (√х)²
х=196;
28 = √х
(28)² = (√х)²
х=784;
При х∈ [196; 784] y∈ [14; 28].
d) Найдите при каких х выполняется неравенство у ≤ 5.
√х <= 5
(√х)² <= (5)²
х <= 25;
Неравенство у ≤ 5 выполняется при х <= 25.
a+b, a+c, a+d, a+e
b+c, b+d, b+e
c+d, c+e
d+e
Сумма этих чисел равна
4(a+b+c+d+e)=-1+2+6+7+8+11+13+14+16+20=96,
т.е. a+b+c+d+e=24. С другой стороны, понятно, что самая маленькая сумма равна -1=a+b, а самая большая d+e=20, значит с=24-20+1=5.
Понятно также, что число а - отрицательное, значит a+c<c, и a+c≠-1, т.к. -1=а+b. Значит a+c=a+5=2, т.е. а=-3. Тогда b=-1-a=2. Очевидно 6=а+d, откуда d=6+3=9, и е=20-d=11.
Итак, эти числа -3, 2, 5, 9, 11.
Их произведение -2970.