ответ: 1
Объяснение:
Члены геометрической последовательности связаны следующим соотношением:
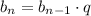
Нам даны три последовательных члена, для определённости дадим им номера 1, 2, 3.
Выпишем взаимосвязь 1-ого и 2-ого и 2-ого и 3-его:
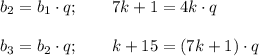
Чтобы три числа были членами последовательности, должны выполнять оба равенства. Составим систему уравнений:
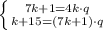
Поделим уравнения друг на друга (это действие можно выполнить, так как q ≠ 0, (7k + 1) ≠ 0, k + 15 ≠ 0):
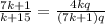
Сокращаем на q ≠ 0 и перемножаем дроби "крест-накрест" (знаменатели в ноль не обращаются, учтено выше).
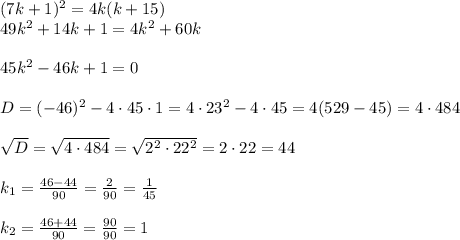
k₁ не является целым, поэтому не подходит. Остаётся один ответ k = 1.
Для построения функции нужно проанализировать ее уравнение.
Очевидно, что функция содержит квадрат аргумента, следовательно, такая функция является квадратной. Графиком же квадратной функции будет парабола.
Узнаем, как будут направлены ветви параболы. Для этого обратим внимание на знак перед х в квадрате. Условно перед ним стоит знак «плюс», а это значит, что ветви параболы будут смотреть вверх.
Также парабола существует для любых значений аргумента х.
Найдем координаты точки, которая является вершиной параболы. Для этого используем известные формулы:
\[x_0=-\frac{b}{2a}=-\frac{0}{2\cdot 1}=0\]
\[y_0=0^2=0\]
Получили вершину данной параболы в начале координат.
В принципе, выше приведенных вычислений можно было и не выполнять, так как мы имеем простейшее уравнение параболы, для которой известно, что она симметрична координатной оси Оу и ее вершина совпадает с точкой (0; 0).
Также необходимо вычислить некоторые точки, которые построить данную параболу.
Подберем любые значения аргумента х и найдем соответствующие им значения функции. Возьмем простейшие значения х, чтобы удобнее было считать:
х = 1: y\left(1\right)=1^2=1 — точка (1; 1).
х = 2: y\left(2\right)=2^2=4 —точка (2; 4).
х = —1: y\left(-1\right)={\left(-1\right)}^2=1 —точка с координатами (—1; 1).
х = —2: y\left(-2\right)={\left(-2\right)}^2=4 —точка с координатами (—2; 4).
Покажем все пять точек на координатной плоскости и соединим их.
от минус бесконечности до точки y₀ - вершины параболы
х₀=-b/2a=-5/2*(-1)=5/2
y₀=- 25/4+ 5*5/2-9=25/4-36/4= -11/4
Е(f)∈(-∞;-11/4)