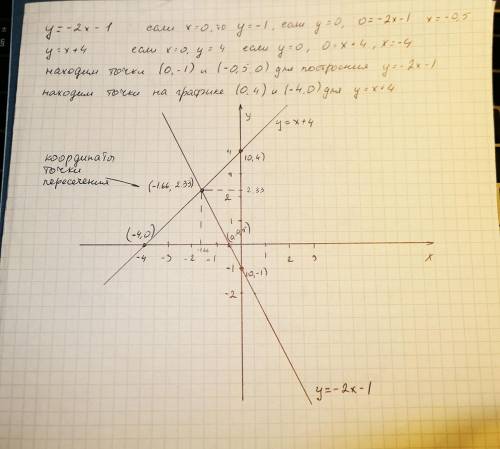
(-1.66 2.33)
Объяснение:
Объяснение:
Любой многочлен степени n вида  представляется произведением постоянного множителя при старшей степени  и n линейных множителей , i=1, 2, …, n, то есть , причем , i=1, 2, …, n являются корнями многочлена.
Эта теорема сформулирована для комплексных корней , i=1, 2, …, n и комплексных коэффициентов , k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.
Если коэффициенты , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.
К примеру, если корни  и  многочлена  являются комплексно сопряженными, а остальные корни действительные, то многочлен представится в виде , где 
1) Так как a и b меньше нуля ,то есть оба отрицательные числа ,то произведение двух отрицательных чисел будут давать только положительный результат
2)Сумма двух любых отрицательных чисел будут давать только отрицательный результат
3)Так как b<a ,то b-a не будет больше 0
Рассмотрим на примере b=-3 ,a=-1=>-3+1<0
4)Так как оба числа являются отрицательными и куб степени а никак не влияет на знак ,то это равносильно произведению двух отрицательных чисел ,которое дают положительный результат
ответ:4
За единичный отрезок берите три клетки, чтобы точку пересечения хорошо было видно.