1. Вычислить A = 2㏒₂㏒₃81+㏒₉√3
решение : 2㏒₂㏒₃81+㏒₉√3 =2㏒₂㏒₃3⁴ + (1/2)㏒₃√3 = 2㏒₂4 + (1/2)*(1/2) =2*2+0,25 = 4,25 .
* * * * * * * * * * * * * * * * * * * *
Не мешает
2.Треугольник ABC имеет стороны AB = 137; AC = 241 и BC = 200. На BC есть точка D, такая, что обе окружности, вписанные в треугольники ABD и ACD, касаются AD в одной точке E. Определите длину CD .
ответ: 152
Пошаговое объяснение:
рисунок приведен во вложении Обозначаем :
DT₁ = DE= DT₂ = y и BK₁ = BT₁ = x .
Используем часть известной теоремы (дальше простоя арифметика )
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности .
AК₂ = AE = AK₁ = AB - BK₁ = 137 - x ;
CT₂ = CK₂ =AC -AK₂ = 241 -(137 - x) = 104 + x .
- - - - - - -
BD + CD = BC BD = BT₁ + DT₁ =x + y ; CD= СT₂ +T₂D ) = 104+x+y
( x + y ) + (104 +x +y) = 200 ⇔ x + y = 48
CD =1 04+ x+y = 104+48 = 152 .
Объяснение:

Биквадратное уравнение.
Решается заменой переменной:

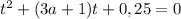
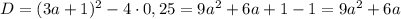
Если D >0, т.е.


уравнение имеет корни:
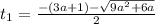 или
или 
Обратный переход:
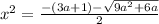 или
или 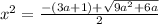
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
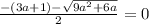
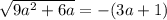
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
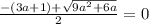
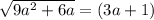
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 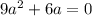
 или
или 
При 
уравнение принимает вид:

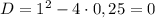 ⇒
⇒ 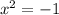
уравнение не имеет корней
При 
уравнение принимает вид:

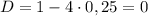 ⇒
⇒ 
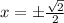
Уравнение 4-ой степени, значит
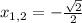 и
и 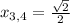
О т в е т. При 
Объяснение:
sin(4*a)/(1 + cos(4*a)) = 2*sin(2*a)*cos(2*a)/( cos^2(2*a) + sin^2(2*a) + cos^2(2*a) - sin^2(2*a)) = 2*sin(2*a)*cos(2*a)/(2*cos^2(2*a)) = sin(2*a)/cos(2*a) = tg(2*a)