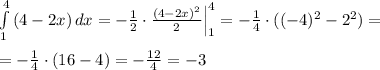
В решении.
Объяснение:
Решить систему уравнений:
а)
ху² - х = 2у
ху² - у = 3х
Выразить ху² через другие члены уравнений:
ху² = 2у + х
ху² = 3х + у
Приравнять правые части уравнений (левые равны):
2у + х = 3х + у
2у - у = 3х - х
у = 2х;
Теперь подставить значение у в любое из двух уравнений:
ху² - х = 2у
х * (2х)² - х = 2 * 2х
4х³ - х = 4х
4х³ - 5х = 0 неполное кубическое уравнение
х(4х² - 5) = 0
х₁ = 0;
4х² - 5 = 0
4х² = 5
х² = 5/4
х = ±√5/4
х₂ = -√5/2;
х₃ = √5/2.
у = 2х
у₁ = 2 * х₁
у₁ = 0;
у₂ = 2 * (-√5/2);
у₂ = -√5;
у₃ = 2 * √5/2;
у₃ = √5;
Решение системы уравнений: (0; 0); (-√5/2; √5); (√5/2; √5).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
в)
х² + у² = 10
х² * у² = 9
Выразить х² через у² во втором уравнении:
х² = 9/у²
Подставить значение х² в первое уравнение и вычислить у:
9/у² + у² = 10
Умножить уравнение (все части) на у², чтобы избавиться от дробного выражения:
9 + у⁴ = 10у²
у⁴ - 10у² + 9 = 0
Ввести новую переменную t:
у² = t, тогда уравнение примет вид:
t² - 10t + 9 = 0, решить как квадратное уравнение:
D=b²-4ac =100 - 36 = 64 √D=8
t₁=(-b-√D)/2a
t₁=(10 - 8)/2
t₁=2/2
t₁=1;
t₂=(-b+√D)/2a
t₂=(10 + 8)/2
t₂=18/2
t₂=9;
Вернуться к первоначальным переменным:
у² = 1
у = ±√1
у₁ = -1;
у₂ = 1;
х² = 9/у²
х = 3/у
х₁ = 3/-1
х₁ = -3;
х₂ = 3/1
х₂ = 3;
у² = 9
у₃ = 3
у₄ = -3
х₃ = 3/3
х₃ = 1;
х₄ = 3/-3
х₄ = -1.
Решение системы уравнений (-3; -1); (3; 1); (1; 3); (-1; -3).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
Відповідь:
а) ні
б) так
в) так
г) ні
Пояснення:
Очевидно, що після додавання до парного числа або віднімання від нього одиниці, отримаємо НЕпарне, і навпаки. Уявімо, що гарбузи вже розкладено. Тоді числа гарбузів у будь-яких двох сусідніх кошиках матимуть різну парність.
Нехай у колі розставлено НЕпарну кількість кошиків. Пронумеруємо їх, скажімо, за годинниковою стрілкою. Почнемо для зручності з довільного кошика із НЕпарною кількістю гарбузів. Побачимо, що таке саме непарне число гарбузів міститиме 3-ій кошик (бо в другому — парна кількість гарбузів), 5-ий, ..., останній. Виходить, що в наступному кошику, який під номером "1", повинно бути парне число гарбузів. Але насправді воно НЕпарне. Отримали суперечність.
А от якби було розставлено парну кількість кошиків, то непарне число гарбузів, пронумерованих, як у попередньому абзаці, містив би ПЕРЕДостанній кошик. Тоді останній — парну, а наступний за ним, кошик під номером "1" — знов непарну, як ми й домовлялися.
Отже, здійснити те, що описано в умові задачі, можна, лише якщо використати парну кількість кошиків.