А) 4√12-10√3=4√(4*3)-10√3=8√3-10√3=-2√3 (1)
Б) -3√27+4√3=-3√(9*3)+4√3=-9√3+4√3=-5√3 (2)
В) 12√3-3√75=12√3-3√(25*3)=12√3-15√3=-3√3 (3)
Объяснение:
1. а) необходимо на место х в дроби подставить заданные значения, т.е.:
при х = 0: (х+3)/(1-4х) = (0+3)/(1-0*4) = 3
при х = -1: (-1+3)/(1-4*(-1)) = 2/5 или же 0,4 это одно и то же
при х = 0,3: (0,3+3)/(1-0,3*4) = 3,3 / (-0,2) = -33/2 = -16,5
при х = -1/4: (-1/4+3)/(1-(-1/4)*4) = (-11/4) / 2 = -11/8
при х = 7: (7+3)/(1-4*7) = 10 / (-27) = - 10/27
при х = 3/2: (3/2+3)/(1-4*(3/2)) = (9/2) / (-5) = -9/10
б) дробь равна нулю, если числитель равен нулю, т.е.:
х + 3 = 0, при х = -3
в) дробь не имеет смысла, если знаменатель равен нулю, что вполне логично, т.к. на 0 делить нельзя, по крайней мере в школе
1 - 4х = 0, х = 1/4
2. а) нужно просто подставить х = -1 и у = 1:
((-1 - 3)^2 + 1^2 -2) / ((2*1 - (-1))*(5 + (-1)^4)) = ((-4)^2 + 1 - 2) / ((2 + 1)*(5 + 1)) = 15 / 18 = 5/6; вычисления в этом пункте лучше еще раз перепроверить
б) здесь можно приравнять скобку в знаменателе к 0:
(2у - х) = 0, при х = 0 и у = 0
t≤2, t≥3
Объяснение:
все выражение находится под корнем. Корень имеет смысл, когда подкоренное выражение больше или равно нулю:
t²-5t+6≥0
найдем корни квадратного трехчлена, для этого приравняем его к нулю:
t²-5t+6=0
по теореме Виета: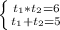 
, откуда корни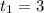 
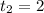
отметим точки на прямой (рис) (закрашенными, т.к наше неравенство нестрогое)
знаки начинаются с +, дальше чередуем.
у нас ≥, выбираем +
t ∈ (-∞; 2] ∪ [3; +∞), что можно понимать, как: нас устраивает t меньше 2 и 2 включительно и больше 3, включая 3 => t≤2, t≥3
Объяснение:
А) 4√12 - 10√3 = 4 · 2 · √3 - 10√3 = 8√3 - 10√3 = - 2√3 соответствует 1
Б) - 3√27 + 4√3 = - 3 · 3√3 + 4√3 = - 9√3 + 4√3 = - 5√3 соответствует 2
В) 12√3 - 3 √75 = 12√3 - 3 · 5√3 = 12√3 - 15√3 = - 3√3 соответствует 3