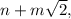где n и m - целые. Второе состоит из всех остальных. Ясно, что оба подмножества непусты, так как первое счетно, а множество действительных чисел несчетно, а если из несчетного множества убрать счетное подмножество, то останется множество той же мощности. Пусть функция во всех точках первого множества принимает какое-то одно значение, скажем 1, а во всех точках второго множества - другое значение, скажем 0. Добавление к числам первого множества любого количества единиц и любого количества корней из 2 не выводит из него. То же справедливо для чисел второго множества, так как если в результате добавления к x числа вида 
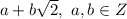получится число вида 
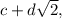, то x равен разности этих чисел, то есть само есть комбинация 1 и корня из 2 с целыми коэффициентами. Поэтому построенная функция удовлетворяет требуемому условию.
Х=4-у, тогда
(4-у)/2=у/3
2-у/2=у/3
2=2у/6+3у/6
2=5у/6
У=12/5=2,4
Х=4-2,4=1,6