ответ: 1) (-4; -1.5) U (¹/₃; +oo) 2) (-oo; -1) U (2; 4)
Объяснение:
подобные неравенства решаются методом интервалов))
что при умножении, что при делении правила получения знака результата одинаковы:
"+" на "+" будет "+";
"-" на "+" будет "-";
"-" на "-" будет "+"... потому решения этих неравенств очень похожи))
главное --найти корни для каждого множителя/делителя или делимого
(2x+3)(3x-1)(x+4) > 0
корни: -1.5; ¹/₃; -4... определяем знак на крайнем правом промежутке (на +бесконечности) --будет "+" и при переходе через корень функция меняет знак (кратных корней нет)
---------(-4)++++++++(-1.5)---------(¹/₃)+++++++
ответ: (-4; -1.5) U (¹/₃; +oo)
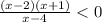
корни: 2; -1; 4... определяем знак на крайнем правом промежутке (на +бесконечности) --будет "+" и при переходе через корень функция меняет знак (кратных корней нет)
---------(-1)++++++++(2)---------(4)+++++++
ответ: (-oo; -1) U (2; 4)
просто складываем:
x+y+2x-y=11-5;
3x=6; x=2; y=11-2=9;
подстановка:
y=11-x, 2x-11+x=-5; 3x=6; x=2;
y=11-2=9;
2) y=5-2x; 3x-10+4x=4; 7x=14; x=2; y=5-4=1;
3) умножаем 1 уравнение на -5 , 2 на 2 и складываем:
-10x-15y+10x-8y=-15+38;
-23y=23;
y=-1; 2x-3=3; 2x=6; x=3