1 1 1
------------------ + ---------------------+ ------------------ <=1
(x+2)(x+3) (x+2)(x+4) x^2+7x+12
1 1 1
---------------- +---------------------- + ------------------------- - 1<=0
(x+2)(x+3) (x+2)(x+4) (x+3)(x+4)
x+4+x+3+x+2-(x+2)(x+3)(x+4)
--------------------------------------------------------- <=0
(x+2)(x+3)(x+4)
3(x+3)-(x+2)(x+3)(x+4)
---------------------------------------- <=0
(x+2)(x+3)(x+4)
(x+3)(3-(x+2)(x+4)
--------------------------------- <=0
(x+2)(x+3)(x+4)
-(x+3)(x²+6x+5)
------------------------------ <=0
(x+2)(x+3)(x+4)
- (x+3)(x+1)(x+5)
------------------------ <=0
(x+2)(x+3)(x+4)
смогла только упростить(((
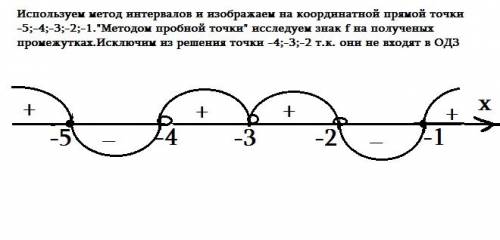
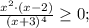
Можно решить методом интервалов: на числовой прямой отмечаем нули числителя и знаменателя - это х = 0 (двойной корень, х = 2 и х = - 3 (четверной корень). Правило: при переходе через корень четной степени, каковыми являются 0 и -3, знак неравенства не меняется. Значит, крайний правый будет +, затем при переходе через два будет -, при переходе через 0 знак остается -, и при переходе через -3 также остается отрицательным. Следовательно, решением данного неравенства будет {0} в объединении с интервалом [2; + бесконечность).
Надеюсь, что все это изобразишь на числовой прямой и поймешь решение!
S₇=b₁·(q⁷-1)/(q-1)=6·(2⁷-1)/(q-1)=6·(128-1)/1=6·127=762