Для лучшего пояснения, пусть товар стоит 100 рублей.
"С какой процентной надбавкой должен продать торговец оставшийся товар чтобы получить 32% надбавку."
Торговцу нужно продать весь товар с надбавкой в 32%.
То есть заработать всего 100*132%=132 рубля.
"Торговец 20% товара продал 40% добавкой."
100*20%=20 рублей. Товар на 20 рублей, он продал с наценкой в 40%
20*140%=28 рублей. Ему надо продать на 132 рубля, 132-28=104 рубля осталось заработать.
"С какой процентной надбавкой должен продать торговец оставшийся товар?"
оставшегося товара 100%-20%=80%, товар стоимость 100*80%=80 рублей, нужно продать за 104 рубля.
104/80=1,3=130%.
Оставшийся товар надо продать за 130%-100%=30% надбавкой.
Проверка: 20%*140%=28% рублей.
80%*130%=104%. 28%+104%=132% 132-100=32% надбавки.
ответ: 30%
К натуральному числу Х справа приписали три цифры, значит, само число увеличили в 1000 раз и добавили к нему некое трёхзначное число А, получилось 1000 Х + А, которое равно сумме всех чисел от 1 до Х.
Запишем эту сумму по-разному, от меньшего к большему, и наоборот. Получатся два верных равенства, которые можно почленно сложить.
1 + 2 + 3 + ... + (Х-2) + (Х-1) + Х = 1000 Х + А
Х + (Х-1) + (Х-2) + ... + 3 + 2 + 1 = 1000 Х + А
------------------------------------------------------------------------
(Х+1)+(Х+1)+(Х+1)+ ... + (Х+1) + (Х+1) + (Х+1)=2(1000 Х + А)
Слева сумма Х одинаковых скобок (Х+1) :
(Х + 1) Х = 2000 Х + 2 А
Разделим обе части равенства на Х (по условию Х - натуральное число, поэтому Х ≠ 0)
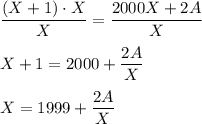
Итак, исходное число Х ≥ 1999.
По условию А - трёхзначное число, максимальное значение которого 999. Тогда 2·999=1998 < 1999. Следовательно, дробь
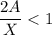для любых трёхзначных чисел А.
Из условия, что число Х - натуральное и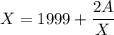 
следует, что число Х = 1999
ответ: Х = 1999
(180°-х)-x=122°
2x=180°-122°
2x=58°
x=29°
180-x=151°
ответ: один угол равен 29°, а другой угол равен 151°.