Определим общее число расстановок на пяти позициях 5 шариков:
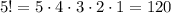
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах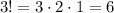 
Таким образом, всего имеется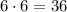 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
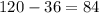
ответ: 84
(x+50)/x>=m
(x+50-mx)/x >= 0
1) {x(1-m) +50>=0 {x >= 50/(m-1) Теперь найдём значение параметра m,
{ x >= 0 { x >= 0 при котором наибольшее положительное
решение неравенства равно 10.
50/(m-1) = 10 > 50 = 10m - 10, 10m = 60, m = 6
2) {x(1-m) +50 <0 Эту систему не решаем так как здесь Х принимает только
{ x < 0 отрицательные значения.
ответ. m = 6
^ -степень
/- дробная черта