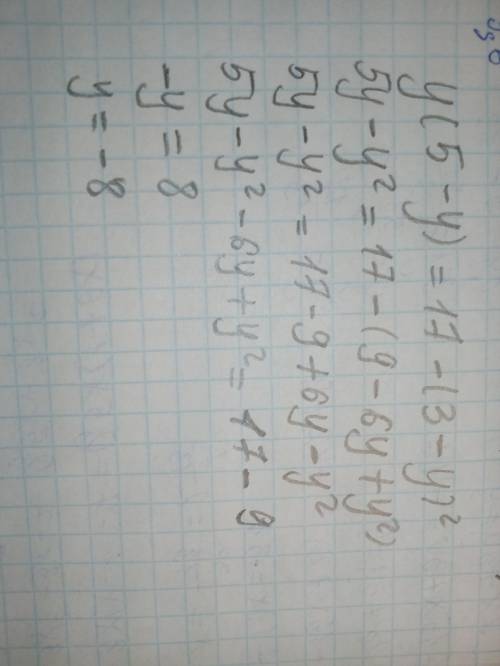
1)
a) x < -5; x ∈ (-∞; -5)
б) x >= -5 ; x ∈ [-5; +∞)
в) x <= - 5 ; x ∈ (-∞; -5]
г) x > - 5; x ∈ (-5; +∞)
ответ : б)
2)
6 - положительное, целое - натуральное
3/7 - нецелое (0 < 3/7 < 1) - не натуральное
√2 - нецелое (1 < √2 < 2) - не натуральное
0 - не положительное - не натуральное
-8 - не положительное - не натуральное
-3,9 - не положительное - не натуральное
37 - положительное, целое - натуральное
п - 3,14 - положительное, целое - натуральное
-√7 - не положительное - не натуральное
ответ: 26, 37, п
3)
3√49 - 3(√2)^2
3√49 = 3*7=21
21 - 3(√2)^2
21 - 3*2 = 21 - 6 = 15
4)
5х-15<0
2x-3>=0
5x<15
2x>=3
x=3
x=3/2=1.5
x е [1.5; 3)
5) 35/3√7 * √7/√7 = 5*7*√7/3*7= 5√7/3
6)
√7×√63 - √27 ÷ √12=
=√441 - √27 ÷ √4 =
= 21 - 3÷2 =
= 39÷2 =
= 19,5
рассмотрим сначала многочлен
5 ⋅ x 2 ⋅ y + 2 ⋅ y 3 − x ⋅ y + 1 5·x2·y+2·y3−x·y+1
: его члены имеют стандартный вид, подобные члены отсутствуют, значит многочлен задан в стандартном виде, и никаких дополнительных действий не требуется.
Теперь разберем многочлен
0 , 8 + 2 ⋅ a 3 ⋅ 0 , 6 − b ⋅ a ⋅ b 4 ⋅ b 5 0,8+2·a3·0,6−b·a·b4·b5
. В его состав входят нестандартные одночлены: 2 ⋅ a 3 ⋅ 0 , 6 и − b ⋅ a ⋅ b 4 ⋅ b 5 2·a3·0,6 и −b·a·b4·b5, т.е. имеем необходимость привести многочлен к стандартному виду, для чего первым действием преобразуем одночлены в стандартный вид: 2 ⋅ a 3 ⋅ 0 , 6 = 1 , 2 ⋅ a 3 2·a3·0,6=1,2·a3; − b ⋅ a ⋅ b 4 ⋅ b 5 = − a ⋅ b 1 + 4 + 5 = − a ⋅ b 10 −b·a·b4·b5=−a·b1+4+5=−a·b10, таким образом получаем следующий многочлен: 0 , 8 + 2 ⋅ a 3 ⋅ 0 , 6 − b ⋅ a ⋅ b 4 ⋅ b 5 = 0 , 8 + 1 , 2 ⋅ a 3 − a ⋅ b 10 0,8+2·a3·0,6−b·a·b4·b5=0,8+1,2·a3−a·b10. В полученном многочлене все члены – стандартные, подобных членов не имеется, значит наши действия по приведению многочлена к стандартному виду завершены.