По определению модуля:
sin(2x+(π/9)) +(1/2)= -1 или sin(2x+(π/9))+(1/2) = 1
sin(2x+(π/9)) +(1/2)= -1 ⇒ sin(2x+(π/9)) = -3/2
уравнение не имеет корней по свойству ограниченности синуса
-1 ≤ sin(2x+(π/9)) ≤1
sin(2x+(π/9)) = 1/2 ⇒2x+(π/9)=(-1)^(k)(π/6)+πk, k∈Z
Удобнее записать в виде двух серий ответов при k=2n и k=2m+1:
2x+(π/9)=(π/6)+2πn, n∈Z или 2x+(π/9)=(-π/6)+2πm+π, m∈Z
2x=(-π/9)+(π/6)+2πn, n∈Z или 2x= (-π/9)+(5π/6)+2πm, m∈Z
2x=(π/18)+2πn, n∈Z или 2x= (13π/18)+2πm, m∈Z
x=(π/36)+πn, n∈Z или x= (13π/36)+πm, m∈Z
О т в е т. (π/36)+πn, n∈Z; (13π/36)+πm, m∈Z
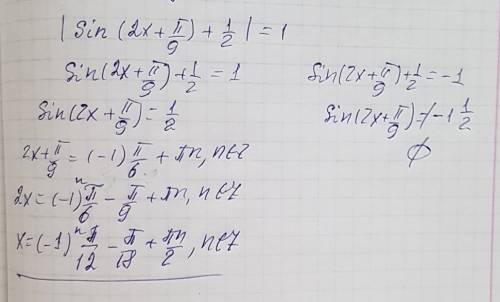
а) у= х²-2х = у= х²-2х *1 + 1 - 1 = (х-2)² -1
На координатной плоскости это парабола с вершиной (2;-1)
Ветви параболы направлены вверх (а=1>0)
Наименьшее значение функции у = -1
б) у=4х²- х+5 = 4х²-2*2х* 1/4 + 1/16 - 1/16 +5 = (2х -1/4)² + 4 15/16
На координатной плоскости это парабола с вершиной (1/4; 4 15/16)
Ветви параболы направлены вверх (а = 4 >0)
Наименьшее значение функции у = 4 15/16
Наименьшее значение функции у = -1
в) 7х-2х² = -2( х² +3,5х) = -2(х² +2х*7/4 + 49/16 - 49/16) = -2( (х +7/4)² -49/16)=
=-2(х+7/4)² + 49/8
На координатной плоскости это парабола с вершиной (-7/4;- 49/8)
Ветви параболы направлены вниз (а= -7/4 <0)
Наименьшее значение данная функция не имеет