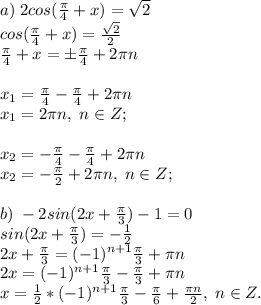
Пусть x - собственная скорость катера, тогда (x-3) - скорость, с которой передвигается катер против течения, а (x+3) - скорость, с которой передвигается катер по течению.
Тогда 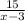 - время, которое катер плыл против течения, а
- время, которое катер плыл против течения, а 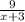 - время, которое катер плыл по течению
- время, которое катер плыл по течению
Полчаса - это 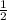 часа
часа
Из условия задачи следует
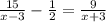
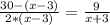
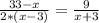

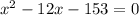
Решаем квадратное уравнение, находим дискриминант:
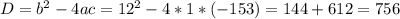
Находим корни:
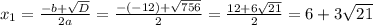
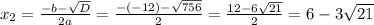
Второй найденный корень - отрицательный, нам не подходит, так как скорость не может быть отрицательной.
Значит, собственная скорость катера 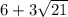 км/ч
км/ч
ответ: собственная скорость катера 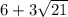 км/ч
км/ч