Пусть задумали число х,приписав справа 6,получим число 10х+6...уравнение 10х+6-х=249...9х=243..х=27,одна треть=9..всё!
Объясняю-задумали 27...приписали 6,получили 276...а 276=27*10+6,поэтому если задумали число х,то приписав 6,получим 10х+6...надеюсь,так понятно?)
Попробуйте взять другое число...например,8,приписав 6,получим 86...просто при приписывании одной цифры справа исходное число переходит из разряда единиц в разряд десятков,т.е.,увеличивается в 10 разтакже и с 27...
При составлении уравнения мы число не знали вообще,оно было равно х...27 мы нашли уже в процессе решения уравнения...если бы было задумано 34,то мы получили бы число 346=340+6=34*10+6также и с 27...276=270+6=27*10+6
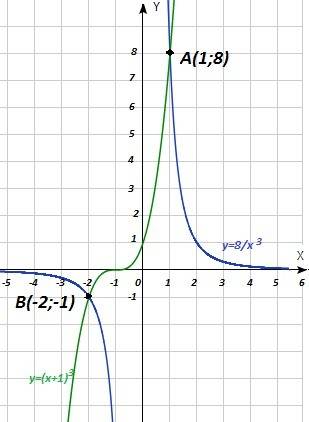
Чтобы решить графически уравнение, нужно построить два графика: для функции слева и функции справа от знака равенства.
1) 
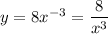- степенная функция с отрицательным показателем (-3) называется гиперболой третьего порядка. Ветви параболы расположены в первой и третьей четвертях (k=8 > 0)
Область определения x≠0 ⇒ x ∈ (-∞; 0) ∪ (0; +∞)
Область значений функции y ∈ (-∞; 0) ∪ (0; +∞)
Точки для построения
x : 1 -1 2 -2 4 -4
y : 8 -8 1 -1 1/8 -1/8
2) y = (x + 1)³ - степенная функция с натуральным показателем. График - кубическая парабола.
Область определения x ∈ R
Область значений функции y ∈ R
Точки для построения
x : 0 1 -1 2 -2 -3
y : 1 8 0 27 -1 -8
Графики представлены в приложении.
Графики пересекаются в двух точках А(1; 8) и B(-2; -1). Координаты х точек пересечения являются решением уравнения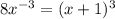 
.
ответ : x₁ = 1; x₂ = -2
Тогда а=2в - длина.
Определим высоту с:
а - 30%
с - 100%
с = 100а/30
с=10а/3 = 20в/3
Sпов=2(а•в+а•с+в•с)
Где а в и с - длина, ширина и высота параллелепипеда.
Уравнение:
2(2в•в + (2в•20в)/3 + (в•20в)/3) =2253,44
2в^2 + (40в^2)/3 + (20в^2)/3 = 126,72
(6в^2)/3 + (60в^2)/3 = 126,72
(66в^2)/3 = 126,72
в^2 = 3•126,72/66
в^2 = 5,76
в = √5,76
в = 2,4 м - ширина
а = 2в = 2•2,4 = 4,8 м - длина
с = 20в/3 = 20•2,4/3 =
= 20•0,8 = 16 м - высота
ответ: а) 2,4 м; 4,8 м; 16м
А второе задание написано не очень понятно. Опубликуйте его точнее и отдельно.