чтобы решить уравнение нужно привести всё к общему знаменателю
х 7 8
___ - =
х-2 х + 2 х² - 4
нижний знаменатель х² - 4 можно разложить по формуле разности квадрата. вы её наверняка проходили.
получится (х-2)(х+2)
всё уравнение имеет вид
х 7 8
___ - =
х-2 х + 2 (х-2)(х+2)
ну а теперь домножаем до одного знаменателя. в первом столбике умножим на (х+2), во втором на (х-2), а третий так и оставим.
получится:
х(х+2) - 7(х-2) - 8
= 0;
(х-2)(х+2)
когда раскроем скобки получится:
х² + 2х - 7х + 14 - 8
= 0;
(х-2)(х+2)
сверху получится х² - 5х + 6 = 0
находим через дискриминант. D = b² - 4ac;
D = 25 - 4*6 = 25-24 = 1;
х₁= -b + √D
= 5 + 1
2a 2
x₁ = 3;
х₂ = 5-1
___ = 2
2
всё уравнение имеет вид
(x-2)(x-3)
= 0;
(х-2)(х+2)
сократив дробь получим
х-3
___ = 0;
х + 2
т.к. делить на ноль нельзя, то х+2 ≠0
х ≠ -2
ответ: х∋(-∞;-2)(-2;+∞)
на самом деле это несложное уравнение, просто я пыталась как можно больше объяснить свои действия :)
1.
а)
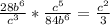
б)
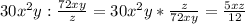
в)
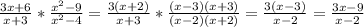
г)
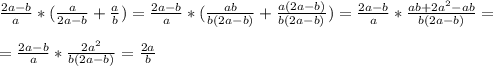
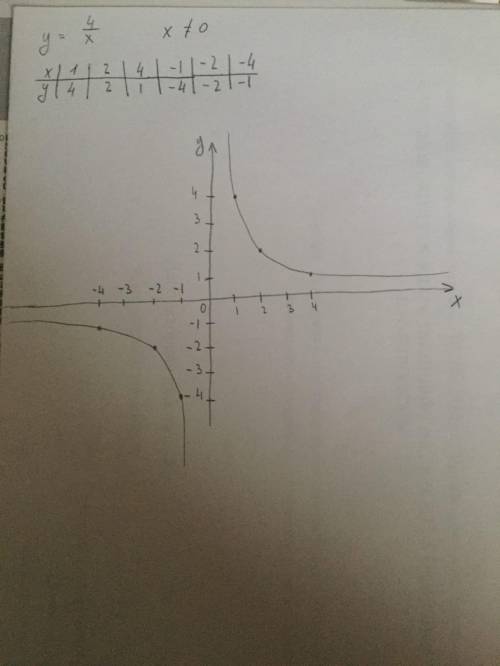
2. График на фото.
Область определения:
D(f)=(-∞;0)∪(0;+∞)
Функция принимает положительные значения при всех положительных Х, кроме 0(так как при нем знаменатель будет равен нулю).
3.
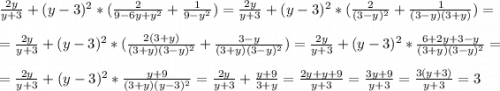
Получаем, что при всех значениях Y(кроме +-3) значение выражение будет равно 3, то есть какой бы Y мы не взяли, данное выражение всегда будет давать в ответе 3, что говорит о том, что оно не зависит от Y.
4.
Данное выражение имеет смысл при всех Х, кроме тех, при которых знаменатель будет равен 0.
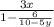
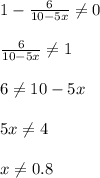
x∈(-∞;0.8)∪(0.8;+∞)
sin3x>0
0<3sin3x≤3 1/3sin3x≥1/3 1/3sin3x+3≥3 1/3
sin3x<0
-3≤3sin3x 1/3sin3x+3≤ -3 1/3
множество значений (-∞;-3 1/3]∪[3 1/3;∞)