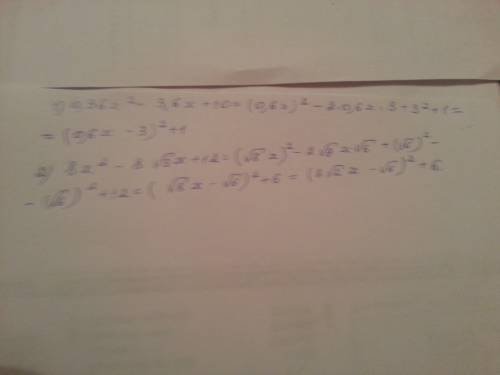
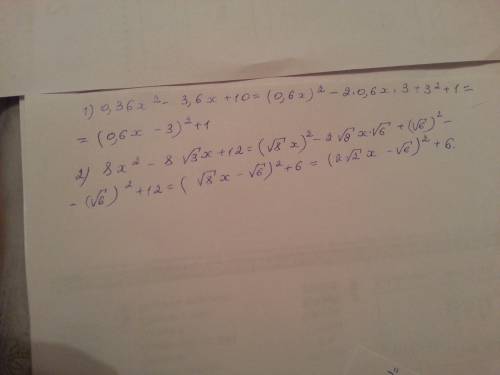
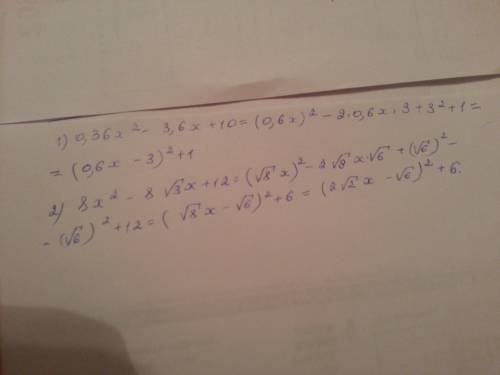
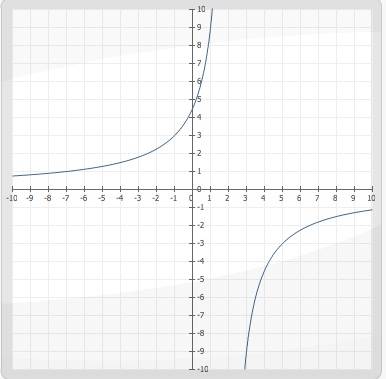
1. Для первого значения аргумента функция является непрерывной, т.к. подставляя значения аргумента в уравнение получим: 9/2 - это число, слудовательно, условие существования функции соблюдено. Для второго - разрывна, так как знаменатель оюращается в ноль, на ноль делить нельзя в школьной программе.
2. Из последнего предложение следует, что точка 2 - точка разрыва функции, тогда сможем найти лево- и правосторонние пределы: lim x to 2- = 9/ 0- = - бесконечность
lim х to 2+ = 9/0+ = + бесконечность
1) 0,36x^2 - 3,6x + 10 = (0,6x)^2 - 2*0,6x*3 + 3^2 - 3^2 + 10
Формула квадрата разности известна: (a-b)^2 = a^2 - 2ab + b^2
В нашем случае a = 0,6x; 3,6x = 2ab = 2*0,6x*b,
отсюда b = 3,6x/(2*0,6x) = 3,6/1,2 = 3.
Значит, нужно в конце прибавить 3^2 = 9, и тут же их отнять обратно.
Так получилась правая часть нашего равенства. Делаем дальше.
(0,6x)^2 - 2*0,6x*3 + 3^2 - 3^2 + 10 = (0,6x - 3)^2 - 9 + 10 = (0,6x - 3)^2 + 1
2) 8x^2 - 8√3*x + 12 = (2√2*x)^2 - 2*(2√2*x)*(√2*√3) + (√6)^2 - (√6)^2 + 12 =
= (2√2*x - √6)^2 - 6 + 12 = (2√2*x - √6)^2 + 6