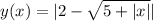
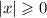


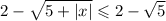

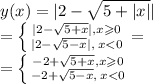
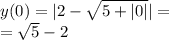
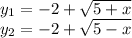
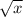
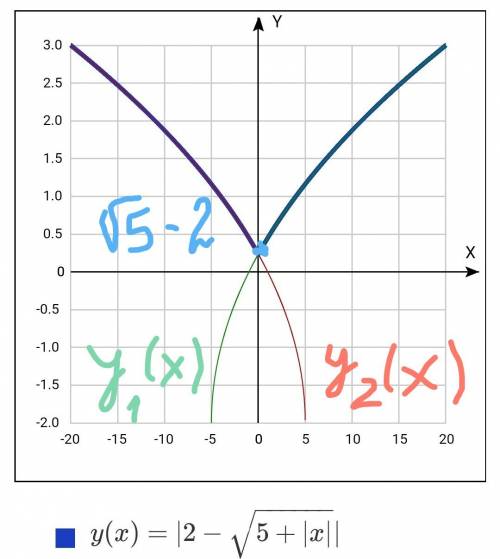
50 км/ч.
Объяснение:
300 : 3 = 100 (км) - проехал поезд до остановки.
300 - 100 = 200 (км) - проехал поезд после остановки.
Пусть х км/ч - скорость поезда до остановки,
тогда (х - 10) км/ч - скорость поезда после остановки.
Составим уравнение:
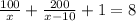
100(x - 10) + 200х + х(х - 10) =8х(х - 10)
100х - 1000 + 200х + х² - 10х = 8х² - 80х
8х² - х² + 10х - 80х - 100х - 200х + 1000 = 0
7х² - 370х + 1000 = 0
D = (- 370)² - 4 * 7 * 1000 = 136900 - 28000 = 108900 = 330²

Второй корень не подходит, так как имея такую скорость, поезд не смог бы её сбросить на 10 км/ч.
Значит, скорость поезда до остановки была 50 км/ч.