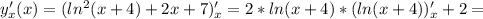
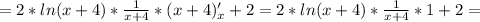
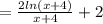
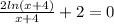
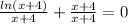
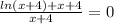
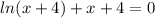
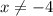 для него сохраняется.
для него сохраняется.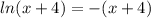
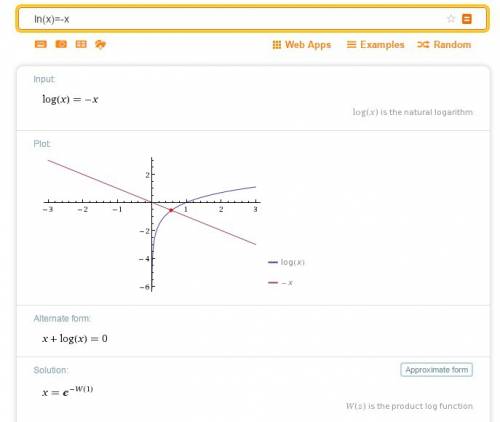
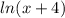 монотонно растет, функция же
монотонно растет, функция же 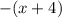 монотонно убывает, что означает, что у уравнения существует лишь один корень.
монотонно убывает, что означает, что у уравнения существует лишь один корень.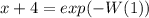
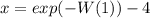
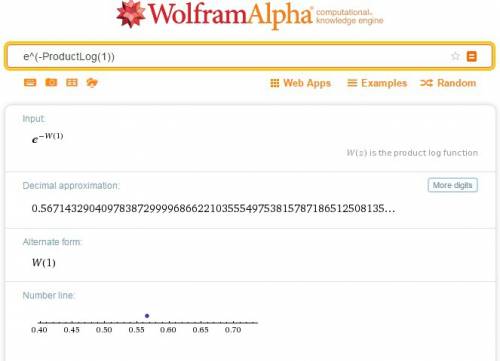
 в бесконечность, действительные значения исследуемой функции также тогда устремятся в бесконечность:
в бесконечность, действительные значения исследуемой функции также тогда устремятся в бесконечность: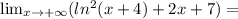
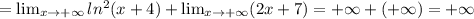
 , она непрерывно растет.
, она непрерывно растет.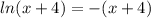
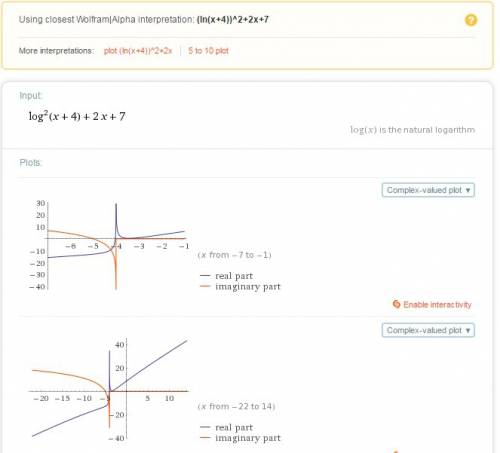
Замена:
ответ: 1; 2