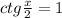
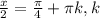∈Z | *2
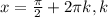∈Z
Відповідь:
РАНОЗАГОЮВАЛЬНІ ПРЕПАРАТИ
Дрібні порізи, опіки і подряпини не потребують стаціонарного лікування під наглядом лікаря, однак ігнорувати їх теж не можна. Використовуючи відповідну мазь для загоєння ран, можна правильно і безпечно для здоров'я вилікувати їх. Таких засобів у аптеках продається безліч, і щоб знати, які саме в яких ситуаціях застосовувати, потрібно розібратися в їх властивостях та особливостях впливу.
Мазі для загоєння ран на шкірі застосовують з давніх давен. Більшість з них виконують відразу кілька функцій: вбивають мікроби і бактерії, створюють захисну плівку, сприяють регенерації тканин. Залежно від глибини порізу або опіку, загоєння займає різний час – від декількох днів до декількох тижнів. Лікарський крем допомагає прискорити цей процес і усунути сліди від ранки.
Мазі для загоєння ран і тріщин використовують при таких пошкодженнях:
-відкриті порізи і подряпини;
-тріщини, викликані сухістю шкіри;
-деякі шкірні захворювання;
-незначні опіки;
-невеликі виразкові ураження.
Важливо розуміти, в яких випадках допустимо самостійне лікування, а коли необхідно звернення до лікаря. Крем для загоєння ран потрібно застосовувати грамотно і не використовувати його при серйозних пошкодженнях. Щоб уникнути ускладнень і попадання інфекції, після його нанесення потрібно накладення стерильної пов'язки.
1) Решить систему линейных уравнений (СЛУ) – это значит найти упорядоченный набор значений всех входящих в неё переменных, который обращает КАЖДОЕ уравнение системы в верное равенство (тождество). Кроме того, система может не иметь решений , то есть быть несовместной.
2) Решение СЛУ с двумя неизвестными представляет собой пару значений двух переменных (х,у) , который обращает КАЖДОЕ уравнение системы в верное равенство. Кроме того, система может быть несовместной (не иметь решений).
3) Система может иметь более одного решения. И если система имеет более одного решения, то таких решений бесчисленное множество .
4) Система может не иметь решения, то есть она будет несовместной.
5) Графический метод решения СЛУ с двумя переменными состоит в том, чтобы начертить графики двух заданных уравнений (это будут прямые). Затем уже по графикам можно делать выводы о количестве решений системы и нахождении их, если они существуют.
6) Если СЛУ с 2 переменными имеет единственное решение, то графики прямых пересекаются в одной точке .
7) Если СЛУ с 2 переменными не имеет решений, то графики прямых параллельны.
8) Если СЛУ с 2 переменными имеет бесчисленное множество решений, то графики прямых совпадают.
