75.
Объяснение:
Пусть х - цифра в разряде единиц,
тогда (х + 2) цифра в разряде десятков.
Искомое двузначное число равно:
(х + 2) * 10 + х = 10х + 20 + х = 11х + 20.
Сумма цифр искомого двузначного числа равна:
х + х + 2 = 2х + 2.
Получаем уравнение:
(11х + 20) * (2х + 2) = 900
22x² + 22x + 40x + 40 = 900
22x² + 62x + 40 - 900 = 0
22x² + 62x - 860 = 0 I : 2
11x² + 31x - 430 = 0
D = 31² - 4 * 11 * (- 430) = 961 + 18920 = 19881
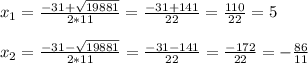
Второй корень не подходит, значит, цифра в разряде единиц равна 5.
Цифра в разряде десятков рана:
5 + 2 = 7.
Искомое двузначное число равно: 75.
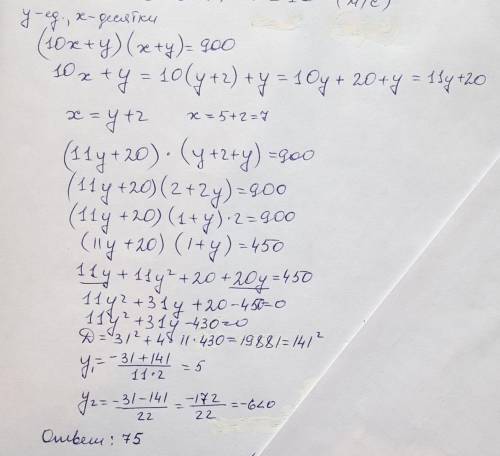
b2+b3=12=>b1q(q+1)=12
b1q(q+1)
=12/8
b1(1-q)
8(q^2+q)=12(1-q)
8q^2+8q-12-12q=0
8q^2+20q-12=0(:4)
2q^2+5q-3=0
(2q-1)(q+3)=0
q=1/2
q=-3
b1=8/(1-q)=8/(1+3)=2
b1=8/(1-1/2)=8/1/2=16
Sn=b1(q^n-1)/q-1
S4=2((-3)^4-1)/-3-1=2*80/-4=-40
S4=16((1/2)^4-1)/1/2-1=16*(-15/16)/-1/2=-15/-1/2=30