Алгебра: не помню как делать cos a/2-sin a/2 при a=п/2 15

Найдите все значения параметра а не имеет корней на промежутке [-√5;2) Преобразуем наше уравнение введем замену переменной тогда уравнение примет вид где t≥0 Для того, чтобы уравнение имело решение, необходимо чтобы D 0 найдем D посмотрим при каких а дискриминант будет больше 0 очевидно что при любых а найдем корни уравнения так как t≥0 проверим наши корни очевидно что этот корень нам не подходит проверив аналогично убедимся что второй корень нам подходит т.е. Теперь найдем корни уравнения так...

не помню как делать cos a/2-sin a/2 при a=п/2 15

👇

Увидеть ответ

Ответ:

васеня220044

28.07.2020

Cos a/2=cos pi/2/2=cos(pi/4)
cos(pi/4)=квадр. корень(2)/2
sin a/2=sin(pi/4)
sin(pi/4)=кор(2)/2
кор(2)/2-кор(2)/2=0
ответ: 0

4,5(53 оценок)

Открыть все ответы

Ответ:

serikon1

28.07.2020

Верно утверждение № 3.

Объяснение:

1) Неверно.

Один из признаков равенства треугольников звучит так: если сторона и два прилежащих к ней угла равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

2) Неверно.

По равенству трех углов (а на самом деле достаточно равенства двух углов) доказывается только подобие треугольников.

3) Верно.

Фраза "не превосходит 90°" означает, что сумма двух острых углов либо равна 90°, либо меньше 90°. Сумма же острых углов в прямоугольном треугольнике равна 90°.

4,4(6 оценок)

Ответ:

143424

28.07.2020

Найдите все значения параметра а

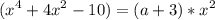
$\displaystyle (x^4+4x^2-10)=(a+3)*x^2$

не имеет корней на промежутке [-√5;2)

Преобразуем наше уравнение

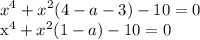
$\displaystyle x^4+x^2(4-a-3)-10=0

x^4+x^2(1-a)-10=0$

введем замену переменной

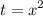
$\displaystyle t=x^2$

тогда уравнение примет вид

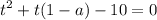$\displaystyle t^2+t(1-a)-10=0$ где t≥0

Для того, чтобы уравнение имело решение, необходимо чтобы D>0
найдем D

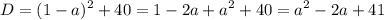
$\displaystyle D=(1-a)^2+40=1-2a+a^2+40=a^2-2a+41$

посмотрим при каких а дискриминант будет больше 0

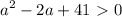
$\displaystyle a^2-2a+41\ \textgreater \ 0

$
очевидно что при любых а

найдем корни уравнения

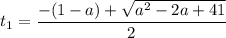
$\displaystyle t_1= \frac{-(1-a)+ \sqrt{a^2-2a+41}}{2}$

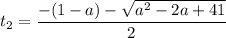
$\displaystyle t_2= \frac{-(1-a)- \sqrt{a^2-2a+41}}{2}$

так как t≥0
проверим наши корни

$\displaystyle a-1- \sqrt{a^2-2a+41}\ \textgreater \ 0$

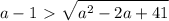
$\displaystyle a-1\ \textgreater \ \sqrt{a^2-2a+41}$

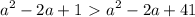
$\displaystyle a^2-2a+1\ \textgreater \ a^2-2a+41$

очевидно что этот корень нам не подходит
проверив аналогично убедимся что второй корень нам подходит
т.е.
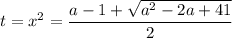
$\displaystyle t=x^2= \frac{a-1+ \sqrt{a^2-2a+41}}{2}$

Теперь найдем корни уравнения

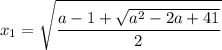
$\displaystyle x_1= \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2}}$

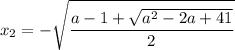
$\displaystyle x_2=- \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2}}$

так как наш промежуток [-√5;2) то положительный корень при любых а не попадет в этот промежуток.
Достаточно рассмотреть только отрицательный корень

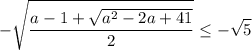
$\displaystyle - \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2}} \leq-\sqrt{5}$
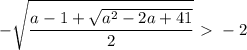
$\displaystyle - \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2} }\ \textgreater \ -2$

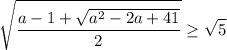
$\displaystyle \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2} } \geq\sqrt{5}$
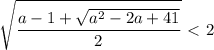
$\displaystyle \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2}}\ \textless \ 2$

решим эти два неравенства
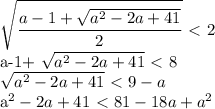
$\displaystyle \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2}}\ \textless \ 2

a-1+ \sqrt{a^2-2a+41} \ \textless \ 8

 \sqrt{a^2-2a+41}\ \textless \ 9-a

a^2-2a+41\ \textless \ 81-18a+a^2$
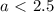
$\displaystyle a\ \textless \ 2.5$

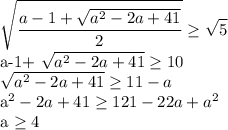
$\displaystyle \sqrt{ \frac{a-1+ \sqrt{a^2-2a+41}}{2}} \geq \sqrt{5}

a-1+ \sqrt{a^2-2a+41} \geq 10

 \sqrt{a^2-2a+41} \geq 11-a

a^2-2a+41 \geq 121-22a+a^2

a \geq 4$

ответ (-оо;2.5)∪[4;+oo)

4,5(36 оценок)

Это интересно:

Финансы-и-бизнес

01.03.2023

10 советов как сэкономить деньги, делая покупки раз в месяц...

Кулинария-и-гостеприимство

28.11.2021

Глазурь без сахарной пудры: простой рецепт и секреты идеальной текстуры...

Образование-и-коммуникации

08.01.2022

Как выглядеть круто в школьной форме...

Дом-и-сад