Изначальное неравенство:
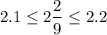
Оно нестрогое, так как скобки квадратные (данный промежуток является отрезком).
Чтобы не мучаться с неправильными дробями, вычтем из всего неравенства двойку. Так делать можно.
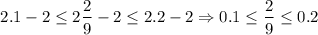
Запишем все в виде обыкновенных дробей
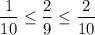
Тут вообще сразу видно, что правая часть неравенства не выполняется (это как при делении пирога: если делить его на большее количество, то каждому меньше достанется)
Чтобы не было недоразумений, докажу это:
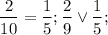
v - некоторый знак неравенства
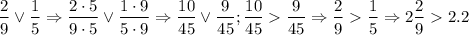
То есть наше число больше правой (большей) границы, а значит, оно НЕ принадлежит отрезку и записывается это таким образом:
![$\boxed{2\frac{2}{9}\notin [2.1; 2.2] }](/tpl/images/0305/3392/a9367.png)
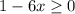 откуда
откуда 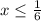 (почему так? Потому что подкоренное выражение должно принимать неотрицательное значение)
(почему так? Потому что подкоренное выражение должно принимать неотрицательное значение)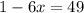

y1=f(x1)+f '(x1)(x-x1) = f '(x1)x +f(x1) -f '(x1)x1
f(x1)=(32/9)(x1-1)^2, f '(x) =(32/9)*3(x-1)^2 =(32/3)(x-1)^2,
f '(x1)=(32/3)(x1-1)^2
2) f(x)=x2, уравнение касательной в какой-либо точке x2:
y2=f(x2)+f '(x2)(x-x2) = f '(x2)x +f(x2) -f '(x2)x2
f(x2)=(x2)^2, f '(x)=2x, f '(x2)=2(x2)
Если касательные общие, значит y1=y2,
значит должны быть равны коэфф. перед x и свободные члены,
получаем систему уравнений с 2 неизвестными:
f '(x1)=f '(x2), f(x1) -f '(x1)x1=f(x2) -f '(x2)x2
1. (32/3)(x1-1)^2=2(x2); 2. (32/9)*(x1-1)^3 -x1*(32/3)(x1-1)^2=(x2)^2 -2(x2)^2
1. ((32/3)(x1-1)^2)/(x2)^2 =2; 2.(((32/3)(x1-1)^2)/(x2)^2)((x1-1)/3 -x1)= -(x2)^2;
подставляя первое в 2, из второго уравнения получаем:
2(x1-1-3x1)/3 = -x2, 2(2x1+1)/3= x2, подставляем в 1.
((32/3)(x1-1)^2=4(2x1+1)/3, 8(x1^2 -2x1+1)=2x1+1,
8x1^2-18x1+7=0, x1=(18+-√100)/16, x1=1/2, x1=7/4
Теперь найдем уравнения касательной y1, они же будут равны =y2:
1. x1=1/2, f(x1)=(32/9)(1/2 -1)^3=(32/9)(-1/2)^3=(32/9)(-1/8)= -4/9
f '(x1)=(32/3)(1/2 -1)^2=(32/3)(1/4) = 8/3
y1= -4/9 + (8/3)(x-1/2) = -4/9 +(8/3)x -8/6, обозначим y1 просто y:
18y=48x-32, 9y=24x-16 - первое уравнение общей касательной
2. x1=7/4, f(x1)=(32/9)(7/4 -1)^3 = (32/9)(3/4)^3=(32/9)(27/64)=3/2,
f '(x1)=(32/3)(7/4 -1)^2= (32/3)(3/4)^2=(32/3)(9/16)= 6
y1=3/2 +6(x -7/4)=3/2+6x -21/2=6x-9, обозначим y1 просто y:
y=6x -9 - второе уравнение общей касательной