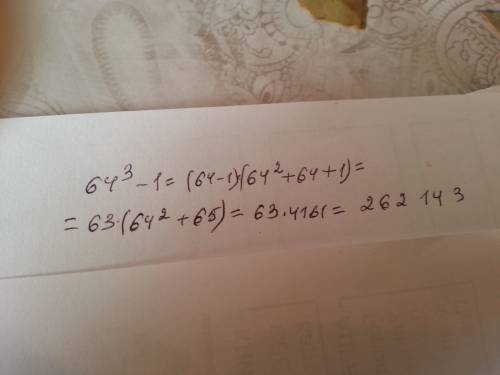
В решении.
Объяснение:
Нужно изучить свойства корней.
а) (2√5 + 3√2)(√5 - √8)=
=(2√5 + 3√2)(√5 - √4*2)=
=(2√5 + 3√2)(√5 - 2√2)=
умножить каждый член первых скобок на каждый член вторых скобок:
=2√5 * √5 + 3√2 * √5 - 2√5 * 2√2 - 3√2 * 2√2 =
= 2 * 5 + 3√10 - 4√10 -6 * 2 =
=10 - 12 - √10 =
= -2 - √10;
б) (√11 - 0,5√22)(0,5√22 + √11) =
умножить каждый член первых скобок на каждый член вторых скобок:
=√11*0,5√22 + √11*√11 - 0,5√22*0,5√22 - 0,5√22*√11 =
=0,5√242 + 11 - 0,5*22 - 0,5√242 =
=0,5√242 + 11 - 11 - 0,5√242 =
=0 (все члены выражения взаимно уничтожаются).
в) (√42)² - (2√6 - 3√2)²=
вторые скобки квадрат разности, по формуле сокращённого умножения:
=42 - [(2√6)² - 2*2√6*3√2 + (3√2)²]=
=42 - (4*6 -12√12 + 9*2)=
=42 - (24 - 12√4*3 + 18)=
=42 - (24 - 12*2√3 + 18)=
=42 - (42 - 24√3)=
=42 - 42 + 24√3=
=24√3.
1-й
Пусть двухместных номеров х, тогда трехместных - (16 - х), в них разместились соответственно 2х и 3(16 - х) туристов. Т.к. туристов всего 42, то составим и решим уравнение
2х + 3(16 - х) = 42,
2х + 48 - 3х = 42,
-х = 42 - 48,
-х = -6,
х = 6.
Значит, двухместных номеров туристы заняли 6, а трехместных:
16 - 6 = 10 (ном.)
ответ: 6 номеров и 10 номеров.
2-й с системы)
Обозначим: х - количество двухместных номеров, y - количество трехместных номеров. По условию составим систему уравнений:
х + y = 16,
2x + 3y = 42.
Выразим из первого уравнения системы переменную х и подставим во второе уравнение:
x = 16 - y,
2(16 - y) + 3y = 42.
Решим получившееся уравнение:
2(16 - y) + 3y = 42,
32 - 2y + 3y = 42,
32 + у = 42,
y = 42 - 32,
у = 10.
Имеем: у = 10, тогда x = 16 - 10 = 6.
Значит, двухместных номеров туристы заняли 6, а трехместных - 10.
ответ: 6 и 10 номеров.