1 вариант
№1
а) (a-5)²=a²-10a+25 б) (6a+b)²=36a²+12ab+b²
в) (4a-1)(4a+1)=16a²-1 в) (a+2b)³=a³+6a²b+6ab²+8b³
№2
(a-6)²-(36+5a)=a²-12a+36-36-5a=a²-17a
№3
а) 3x²+9xy=3x(x+3y) б) 10x⁵-5x=5x(2x⁴-1)
№4
а) (a+3)-2(a+3)=(a+3)(1-2)=-1(a+3) б) ax-ay+5x-5y=a(x-y)+5(x-y)=(x-y)(a+5)
в) a²+4ab+4b²=(a+2b)²=(a+2b)(a+2b)
№5
а) (y²-2a)(2a+y²)=y⁴-4a²
б) (3x²+x)²=9x⁴+6x³+x²
№6
а) 4x²y²-9a⁴=(2xy+3a²)(2xy-3a²) б) 25a²-(a+3)²=(5a-a-3)(5a+a+3)=(4a-3)(6a+3)
в) 27m³+n³=(3m+n)(9m²-3mn+n²)
№7
а) 9y²-25=0
9y²=25
y²=25/9
y₁,₂=±5/3=±1 2/3
б) (x+2)(x-2)-(x-3)²=-1
x²-4-x²+6x-9=-1
6x=12
x=2
№8
а) 35²-25²=(35-25)(35+25)=10*60=600
б) 299*301=299(300+1)=89700+299=8999
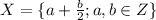
Если взять a=0, b=1, то получается элемент 1/2, квадрат которого равен 1/4 и поэтому не лежит в X. Таким образом, обычное умножение выводит из этого множества, и поэтому не имеет права претендовать на гордое название "алгебраической операции". После этого смешно говорить про ассоциативность (а она бы была, если бы операция не выводила бы из X), про коммутативность (а она бы... - см. текст выше), наличие нейтрального элемента (см. выше). Не знаю, какие элементы Вы называете симметричными, обычно говорят про обратные, но здесь с обратными проблема. В общем, говорить о группе не приходится, как и о группоиде, полугруппе или моноиде
3) там 45+15=60 коробок
4) 12км 250 метров
5)40 страниц
7) 2 км
9)11400 рублей
11) на 10 %
Остальное извини не знаю (подольше подумать надо)