ответ: -2
Объяснение:
Поскольку левая часть уравнения неотрицательна, то раз |x-7| в правой части неотрицательно, то -(x^2+6x+8) >= 0
При выполнении этого условия, данное уравнение из свойства модуля равносильно следующему:
|(x-7)(x^2+6x+8)| = |(x-7)*(- (x^2+6x+8))|
|(x-7)(x^2+6x+8)| = |(x-7)(x^2+6x+8)|
Иначе говоря, уравнение обращается в тождество, а значит решения этого уравнения эквивалентны всем решениям неравенства:
-(x^2+6x+8) >= 0
+ решение x= 7
x^2 +6x + 8 <=0
(x+4)(x+2) <=0
x∈[-4; - 2]
Тогда сумма целых решений:
s= (-4)+ (-3) + (-2) + 7 = -2
Найдем сумму первых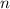 
натуральных чисел по формуле сумме первых 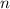членов арифметической прогрессии:
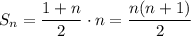
Рассмотрим числитель дроби: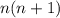 
- произведение двух подряд идущих натуральных чисел, значит одно из них четное, а другое нечетное. Если четное число делится только на 2, но не делится на 4, то при вычислении значения дроби множитель "2" сократится и получившийся результат будет нечетным. Если четное число делится хотя бы на 4, то при вычислении значения дроби один множитель "2" сократится, но еще как минимум один множитель "2" останется и результат будет четным.
Итак, для четного результата сложения необходимо, чтобы хотя бы один из множителей произведения 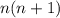делился на 4.
1 случай: 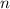делится на 4 (или же можно сказать, что 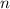при делении на 4 дает остаток 0).
2 случай: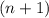 
делится на 4, тогда 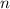при делении на 4 дает остаток 3.
Если эти условия не выполняются, то результат сложения будет нечетным. То есть, можно сказать, что это происходит, когда 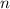при делении на 4 дает остаток 1 или 2.
ответ: четный результат - когда 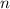при делении на 4 дает в остатке 0 или 3; нечетный результат - когда 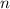при делении на 4 дает в остатке 1 или 2.
5х²-8х-4=0
Дискриминат= b²-4ac=64+80=144
x1,2=-b±√D/2a=8±12/10=2;-4/10=-2/5
Корни 2 и -2/5
Средне арифметическое= 2+(-2/5)/2=4/5